
【題目】為了解本校九年級學生期末數學考試情況,小亮在九年級隨機抽取了一部分學生的期末數學成績為樣本,分為A(100~90分)、B(89~80分)、C(79~60分)、D(59~0分)四個等級進行統計,并將統計結果繪制成如下統計圖,請你根據統計圖解答以下問題:
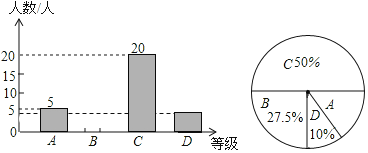
(1)這次隨機抽取的學生共有 人;
(2)這個學校九年級共有學生1200人,若分數為80分(含80分)以上為優秀,請估計這次九年級學生期末數學考試成績為優秀的學生人數大約有 人;
(3)D等級的四位學生正好是兩位男生和兩位女生,小亮想隨機采訪其中的兩位,請用樹狀圖或列表法計算小亮采訪的學生恰好是一男一女的概率.
【答案】(1)40;(2)480;(3)![]() .
.
【解析】
(1)根據C等級人數及其所占百分比可得總人數;
(2)先用被調查的總人數乘以B等級對應百分比求出其人數,再用總人數乘以樣本中A、B等級人數和所占比例即可得;
(3)畫樹狀圖得出所有等可能的情況數,找出一男一女的情況數,即可求出所求的概率.
解:(1)這次隨機抽取的學生共有20÷50%=40(人),
故答案為:40;
(2)B等級人數為40×27.5%=11(人),
∴估計這次九年級學生期末數學考試成績為優秀的學生人數大約有1200×![]() =480(人),
=480(人),
故答案為:480;
(3)畫樹狀圖如下:
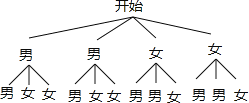
所有等可能的情況有12種,其中一男一女有8種,
所以小亮采訪的學生恰好是一男一女的概率為![]() =
=![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:初中數學 來源: 題型:
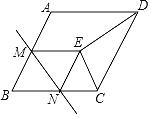
【題目】如圖,在菱形ABCD中,∠B=60°,AB=2,M為邊AB的中點,N為邊BC上一動點(不與點B重合),將△BMN沿直線MN折疊,使點B落在點E處,連接DE、CE,當△CDE為等腰三角形時,BN的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形ABCD,點M為邊AB的中點.
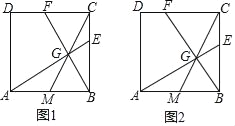
(1)如圖1,點G為線段CM上的一點,且∠AGB=90°,延長AG、BG分別與邊BC、CD交于點E、F.
①求證:BE=CF;
②求證:BE2=BCCE.
(2)如圖2,在邊BC上取一點E,滿足BE2=BCCE,連接AE交CM于點G,連接BG并延長交CD于點F,求tan∠CBF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解學生假期的課外閱讀情況,某校隨機抽查了八年級學生閱讀課外書的冊數并作了統計,繪制出如下統計圖,其中條形統計圖因為破損丟失了閱讀5冊書的數據,根據以上信息,解答下列問題:
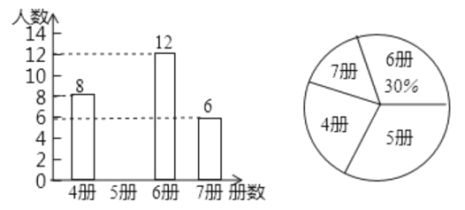
(1)請補全條形統計圖中丟失的數據和扇形統計圖;
(2)閱讀課外書冊數的眾數為______冊;
(3)根據隨機抽查的這個結果,請估計該校1200名學生中課外書閱讀7冊書的學生人數?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對任意一個四位數![]() ,如果千位與十位上的數字之和為7,百位與個位上的數字之和也為7,那么稱
,如果千位與十位上的數字之和為7,百位與個位上的數字之和也為7,那么稱![]() 為“上進數”.
為“上進數”.
(1)寫出最小和最大的“上進數”;
(2)一個“上進數”![]() ,若
,若![]() ,且使一元二次方程
,且使一元二次方程![]() 有兩個不相等的實數根,求這個“上進數”.
有兩個不相等的實數根,求這個“上進數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在菱形ABCD中,∠A=120°,點E是BC邊的中點,點P是對角線BD上一動點,設PD的長度為x,PE與PC的長度和為y,圖2是y關于x的函數圖象,其中H是圖象上的最低點,則a+b的值為( )
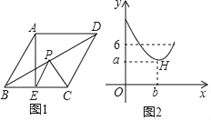
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,對于任意三點A,B,C,給出如下定義:若矩形的任何一條邊均與某條坐標軸平行或重合,且A,B,C三點都在矩形的內部或邊界上,則稱該矩形為點A,B,C的外延矩形,點A,B,C的所有外延矩形中,面積最小的矩形稱為點A,B,C的最佳外延矩形.例如,圖①中的矩形A1B1C1D1,A2B2C2D2,A3B3CD3,都是點A,B,C的外延矩形,矩形A3B3CD3是點A,B,C的最佳外延矩形.
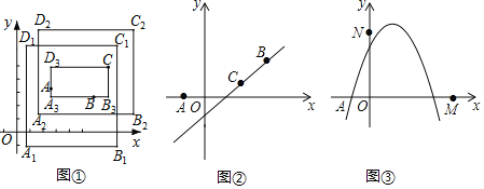
(1)如圖②,已知A(﹣1,0),B(3,2),點C在直線y=x﹣1上,設點C的橫坐標為t.
①若t=![]() ,則點A,B,C的最佳外延矩形的面積為多少?
,則點A,B,C的最佳外延矩形的面積為多少?
②若點A,B,C的最佳外延矩形的面積為9,求t的值.
(2)如圖③,已知點M(4,0),N(0,![]() ),P(x,y)是拋物線y=﹣x2+2x+3上一點,求點M,N,P的最佳外延矩形面積的最小值,以及此時點P的橫坐標x的取值范圍;
),P(x,y)是拋物線y=﹣x2+2x+3上一點,求點M,N,P的最佳外延矩形面積的最小值,以及此時點P的橫坐標x的取值范圍;
(3)已知D(1,0).若Q是拋物線y=﹣x2﹣2mx﹣m2+2m+1的圖象在﹣2≤x≤1之間的最高點,點E的坐標為(0,4m),設點D,E,Q的最佳外延矩形的面積為S,當4≤S≤6時,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四邊形ACDE是平行四邊形,連結CE交AD于點F,連結BD交CE于點G,連結BE. 下列結論中:① CE=BD; ②△ADC是等腰直角三角形;
③∠ADB=∠AEB; ④ CD·AE=EF·CG;
一定正確的結論有
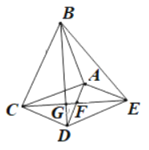
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有四張背面相同的紙牌A、B、C、D,其正面上方分別畫有四個不同的幾何圖形,下方寫有四個不同算式,小明將四張紙牌背面朝上洗勻后摸出一張,將其余3張洗勻后再摸出一張.
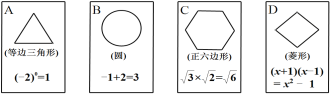
(1)用樹狀圖(或列表法)表示兩次摸牌所有可能出現的結果(紙牌用A、B、C、D表示);
(2)求摸出的兩張紙牌的圖形是中心對稱圖形且算式也正確的紙牌的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com