
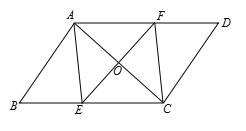
【題目】如圖,在ABCD中,AC的垂直平分線分別交BC、AD于點E、F,垂足為O,連接AE、CF.
(1)求證:四邊形AECF為菱形;
(2)若AB=5,BC=7,則AC= 時,四邊形AECF為正方形.
【答案】(1)見解析;(2)3![]() 或4
或4![]() .
.
【解析】
(1)先根據四邊形ABCD為平行四邊形可得AD∥BC,進而可得∠1=∠2,再根據EF垂直平分AC可得AF=CF,AE=CE,進而可得∠2=∠3,再根據四邊相等的四邊形是菱形作出判定;
(2)當∠AEC=90°時,四邊形AECF是正方形,設AE=EC=x,則BE=7-x,AC=![]() ,根據勾股定理列出方程求得x的值,進而得AC的長即可.
,根據勾股定理列出方程求得x的值,進而得AC的長即可.
(1)證明:∵四邊形ABCD是平行四邊形,
∴AD∥BC,
∴∠1=∠2,
∵EF垂直平分AC,
∴AF=CF,AE=CE,
∵AE=CE,EF⊥AC,
∴∠2=∠3,
∴∠1=∠3,
∴AE=AF,
∴AE=AF=CE=CF,
∴四邊形AECF是菱形.
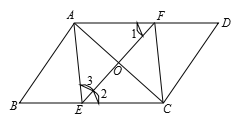
(2)解:∵四邊形AECF是菱形,
∴當∠AEC=90°時,四邊形AECF是正方形,
則∠AEB=90°,
設AE=EC=x,則BE=7-x,AC=![]() ,
,
在Rt△ABE中,![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() ,
,
∴AC=![]() 或
或![]() ,
,
故答案為:3![]() 或4
或4![]() .
.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB=DB,∠1=∠2,請問添加下面哪個條件不能判斷△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三角板是我們學習數學的好幫手.將一對直角三角板如圖放置,點C在FD的延長線上,點B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,則CD的長度是_____.
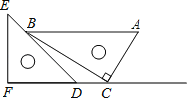
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 經過
經過![]() ,
,![]() 兩點,與
兩點,與![]() 軸正半軸交于點
軸正半軸交于點![]() .
.
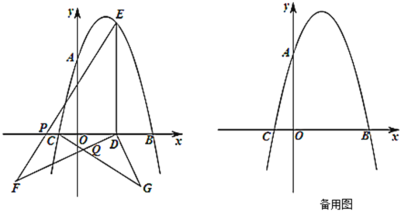
(1)求拋物線的解析式;
(2)![]() 為線段
為線段![]() 上一點,過
上一點,過![]() 作
作![]() 軸的垂線,交拋物線于點
軸的垂線,交拋物線于點![]() ,將線段
,將線段![]() ,
,![]() 繞點
繞點![]() 逆時針旋轉任意相同的角到
逆時針旋轉任意相同的角到![]() ,
,![]() 的位置,使點
的位置,使點![]() ,
,![]() 的對應點
的對應點![]() ,
,![]() 都在
都在![]() 軸下方,
軸下方,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 軸交于點
軸交于點![]() .當
.當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(3)![]() 在拋物線上,
在拋物線上,![]() 在坐標平面內,當以
在坐標平面內,當以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為矩形時,直接寫出點
為頂點的四邊形為矩形時,直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子中裝有三張卡片,分別標有數字1,2,3,這些卡片除數字不同外其余均相同.小明從盒子中隨機抽取一張卡片記下數字后放回,洗勻后再隨機抽取一張卡片.用畫樹狀圖或列表的方法,求第二次抽取卡片上的數字小于第一次抽取卡片上的數字的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古代數學家劉徽將勾股形(古人稱直角三角形為勾股形)分割成一個正方形和兩對全等的三角形,如圖所示,已知∠A=90°, BD=4,CF=6, 則AO的長是 ( )

A.![]() B.
B.![]() C.
C.![]() D.4
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明在某次作業中得到如下結果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=![]() +
+![]() =1.
=1.
據此,小明猜想:對于任意銳角α,均有sin2α+sin2(90°-α)=1.
(1)當α=30°時,驗證sin2α+sin2(90°-α)=1是否成立;
(2)小明的猜想是否成立?若成立,請給予證明;若不成立,請舉出一個反例.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在新冠疫情防控期間,某醫療器械商業集團新進了40臺A型電子體溫測量儀,60臺B型電子體溫測量儀,計劃調配給下屬的甲、乙兩個連鎖店銷售,其中70臺給甲連鎖店,30臺給乙連鎖店.兩個連鎖店銷售這兩種測量儀每臺的利潤(元)如下表:
A型 | B型 | |
甲連鎖店 | 200 | 170 |
乙連鎖店 | 160 | 150 |
設集團調配給甲連鎖店![]() 臺A型測量儀,集團賣出這100臺測量儀的總利潤為
臺A型測量儀,集團賣出這100臺測量儀的總利潤為![]() (元).
(元).
(1)求![]() 關于
關于![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的取值范圍:
的取值范圍:
(2)為了促銷,集團決定僅對甲連鎖店的A型測量儀每臺讓利![]() 元銷售,其他的銷售利潤不變,并且讓利后每臺A型測量儀的利潤仍然高于甲連鎖店銷售的每臺B型測量儀的利潤,問該集團應該如何設計調配方案,使總利潤達到最大?
元銷售,其他的銷售利潤不變,并且讓利后每臺A型測量儀的利潤仍然高于甲連鎖店銷售的每臺B型測量儀的利潤,問該集團應該如何設計調配方案,使總利潤達到最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com