【題目】商場銷售甲、乙兩種商品，它們的進價和售價如表，
進價（元） | 售價（元） | |
甲 | 15 | 20 |
乙 | 35 | 43 |
（1）若該商場購進甲、乙兩種商品共100件，恰好用去2700元，求購進甲、乙兩種商品各多少件？
（2）該商場為使銷售甲、乙兩種商品共100件的總利潤（利潤=售價﹣進價）不少于750元，且不超過760元，請你幫助該商場設計相應的進貨方案．
【答案】
（1）解：設該商場購進甲種商品x件，根據題意可得：
15x+35（100﹣x）=2700，
解得：x=40，
乙種商品：100﹣40=60（件），
答：該商場購進甲種商品40件，乙種商品60件
（2）解：設該商場購進甲種商品a件，則購進乙種商品（100﹣a）件，根據題意得：
，
解得 
≤a≤ 
，
∵a是正整數，
∴a=14，15，16，
∴進貨方案有三種：
方案一：購進甲種商品14件，購進乙種商品86件；
方案二：購進甲種商品15件，購進乙種商品85件；
方案三：購進甲種商品16件，購進乙種商品84件
【解析】（1）首先設出未知數，根據題意可得兩個等量關系：①甲、乙兩種商品共100件；②進價用去2700元；可以列出方程組，解方程組即可；（2）設該商場購進甲種商品a件，則購進乙種商品（100﹣a）件，根據題意得：750≤甲商品的利潤×數量+乙商品的利潤×數量≤760，解不等式組即可；
【考點精析】根據題目的已知條件，利用一元一次不等式組的應用的相關知識可以得到問題的答案，需要掌握1、審：分析題意，找出不等關系；2、設：設未知數；3、列：列出不等式組；4、解：解不等式組；5、檢驗：從不等式組的解集中找出符合題意的答案；6、答：寫出問題答案．
科目：初中數學 來源： 題型：
【題目】我校學生會組織學生到距學校6千米的敬老院打掃衛生，如圖所示，11、12分別表示步行和騎車同學前往目的地所走的路程y（千米）與所用時間x（分鐘）之間的函數圖象，求在距學校多遠處騎車的同學追上步行的同學，此時步行的同學走了多少分鐘？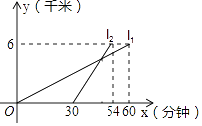 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于x，y定義一種新運算“*”：x*y=3x﹣2y，等式右邊是通常的減法和乘法運算，如2*5=3×2﹣2×5=﹣4，那么（x+1）*（x﹣1）≥5的解集是________．
查看答案和解析>>
科目：初中數學 來源： 題型：
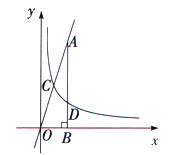
【題目】如圖，反比例函數
(
，)的圖象與直線
相交于點C，過直線上點A(1，3)作AB⊥x軸于點B，交反比例函數圖象于點D，且AB=3BD．
（1）求k的值；
（2）求點C的坐標；
（3）在y軸上確定一點M，使點M到C、D兩點距離之和d=MC+MD最小，求點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某中學對全校學生進行文明禮儀知識測試，為了解測試結果，隨機抽取部分學生的成績進行分析，將成績分為三個等級：不合格、一般、優秀，并繪制成如下兩幅統計圖（不完整）．
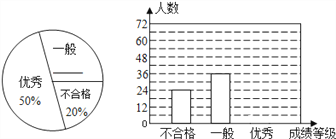
請你根據圖中所給的信息解答下列問題：
（1）請將以上兩幅統計圖補充完整；
（2）若“一般”和“優秀”均被視為達標成績，則該校被抽取的學生中有達標率為 ；
（3）若該校學生有學生3000人，請你估計此次測試中，全校達標的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在數學表達式：（1）﹣3＜0（2）3x+5＞0（3）x2﹣6（4）x=﹣2（5）y≠0（6）x≥50中，不等式的個數是（）
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知點A（0，1），B（2，0），C（4，3）
（1）畫出△ABC，請求△ABC的面積；
（2）設點P在坐標軸上，且△ABP與△ABC的面積相等，求P點的坐標． 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
