
【題目】如圖,在四邊形ABCD中,AD∥BC,∠B﹦90°,AB﹦8cm,AD﹦24cm,BC﹦26cm,點p從點A出發,以1cm/s的速度向點D運動;點Q從點C同時出發,以3cm/s的速度向點B運動,規定其中一個動點到達端點時,另一個動點也隨之停止運動.設運動時間為t s. 
(1)t為何值時,四邊形PQCD為平行四邊形?
(2)t為何值時,四邊形PQCD為等腰梯形?(等腰梯形的兩腰相等,兩底角相等)
【答案】
(1)解:運動時間為ts.
AP=t,PD=24﹣t,CQ=3t,
∵經過ts四邊形PQCD平行四邊形
∴PD=CQ,即24﹣t=3t,解得t=6.
當t=6s時,四邊形PQCD是平行四邊形
(2)解:如圖,過點D作DE⊥BC,則CE=BC﹣AD=2cm
∵當CQ﹣PD=4時,四邊形PQCD是等腰梯形.即3t﹣(24﹣t)=4,
∴t=7.
∴經過7s四邊形PQCD是等腰梯形.

【解析】(1)根據題意可得PA=t,CQ=3t,則PD=AD﹣PA=24﹣t,當PD=CQ時,四邊形PQCD為平行四邊形,可得方程24﹣t=3t,解此方程即可求得答案;(2)過點D作DE⊥BC,則CE=BC﹣AD=2cm當CQ﹣PD=4時,四邊形PQCD是等腰梯形.即3t﹣(24﹣t)=4,求出t的值即可.
【考點精析】通過靈活運用平行四邊形的判定與性質和等腰梯形的性質,掌握若一直線過平行四邊形兩對角線的交點,則這條直線被一組對邊截下的線段以對角線的交點為中點,并且這兩條直線二等分此平行四邊形的面積;等腰梯形的兩腰相等;同一底上的兩個角相等;兩條對角線相等即可以解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子有6個完全一樣的球,分別寫著數字1、2、3、4、5、6,從中摸出一個記下球上的數字,然后放進去,在摸一個球,則兩次摸出球上的數字之和為5的概率為__________。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一元二次方程ax2+bx+c=0中的a=3,b=0,c=﹣2,則這個一元二次方程是( )
A.3x2﹣2=0B.3x2+2=0C.3x2+x=0D.3x2﹣x=0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,O是矩形ABCD的對角線的交點,作DE∥AC,CE∥BD,DE、CE相交于點E.求證: 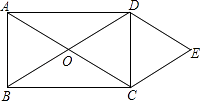
(1)四邊形OCED是菱形.
(2)連接OE,若AD=4,CD=3,求菱形OCED的周長和面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一箱規格相同的紅、黃兩種顏色的小塑料球共1000個.為了估計這兩種顏色的球各有多少個,小明將箱子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回箱子中,多次重復上述過程后.發現摸到紅球的頻率約為0.6,據此可以估計紅球的個數約為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的邊BC與x軸重合,連接對角線BD交y軸于點E,過點A作AG⊥BD于點G,直線GF交AD于點F,AB、OC的長分別是一元二次方程x-5x+6=0的兩根(AB>OC),且tan∠ADB=![]() .
.
(1)求點E、點G的坐標;
(2)直線GF分△AGD為△AGF與△DGF兩個三角形,且S△AGF:S△DGF =3:1,求直線GF的解析式;
(3)點P在y軸上,在坐標平面內是否存在一點Q,使以點B、D、P、Q為頂點的四邊形是矩形?若存在,請直接寫出點Q的坐標;若不存在,請說明理由.
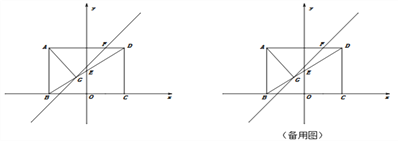
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】6月5日是世界環境日,為了普及環保知識,增強環保意識,某市第一中學舉行了“環保知識競賽”,參賽人數1000人,為了了解本次競賽的成績情況,學校團委從中抽取部分學生的成績(滿分為100分,得分取整數)進行統計,并繪制出不完整的頻率分布表和不完整的頻數分布直方圖如下:

(1)直接寫出a的值,并補全頻數分布直方圖.
分組 | 頻數 | 頻率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成績在80分以上(含80分)為優秀,求這次參賽的學生中成績為優秀的約為多少人?
(3)若這組被抽查的學生成績的中位數是80分,請直接寫出被抽查的學生中得分為80分的至少有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2014年博鰲亞洲論壇年會開幕大會上,中國全面闡述了亞洲合作政策,并特別強調要推進“一帶一路”的建設,中國將出資400億美元設絲路基金.用科學記數法表示400億美元為美元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com