
【題目】如圖,在四邊形ABCD中,AD∥BC,E是AB的中點,連接DE并延長交CB的延長線于點F,點M在BC邊上,且∠MDF=∠ADF。
(1)求證:△ADE≌△BFE;
(2)如果FM=CM,求證:EM垂直平分DF.

【答案】(1)見解析 (2)見解析
【解析】
(1)根據AD∥BC,可得∠ADE=∠F,由E是AB的中點,可得AB=BE,從而可以證明△ADE≌△BFE;
(2)由△ADE≌△BFE,可得DE=EF,再根據∠MDF=∠ADF,AD∥BC,可以得到∠F=∠MDF ,則MF=MD,然后根據等腰三角形三線合一,可以證明結論成立.
證明:(1)∵E是AB的中點,
∴AE=BE,
∵AD∥BC,
∴∠ADF=∠F,
在△ADE與△BFE中
∠ADF=∠F,∠AED=∠BEF,AE=BE,
∴△ADE≌△BFE(AAS);
(2)∵△ADE≌△BFE,
∴DE=EF,
∵AD∥BC,∠ADF=∠F,∠GDF=∠ADF,
∴∠F=∠MDF,
∴MF=MD,
∴△MFD為等腰三角形,
∵DE=EF,
∴EM垂直平分DF.


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:
【題目】七年級某班為準備科技節表彰的獎品,計劃從友誼超市購買筆記本和水筆共40件,在獲知某網店有“五一”促銷活動后,決定從該網店購買這些獎品.已知筆記本和水筆在這兩家商店的零售價分別如下表,且在友誼超市購買這些獎品需花費90元.
品名商店 | 筆記本(元/件) | 水筆(元/件) |
友誼超市 | 2.4 | 2 |
網店 | 2 | 1.8 |
(1)請求出需購買筆記本和水筆的數量;
(2)求從網店購買這些獎品可節省多少元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出下列說法:①射線是軸對稱圖形;②角的平分線是角的對稱軸;③軸對稱圖形的對稱點一定在對稱軸的兩側;④平行四邊形是軸對稱圖形;⑤平面上兩個全等的圖形一定關于某條直線對稱,其中正確的說法有( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】操作:在![]() 中,
中,![]() ,
,![]() ,將一塊等腰直角三角板的直角頂點放在斜邊
,將一塊等腰直角三角板的直角頂點放在斜邊![]() 的中點
的中點![]() 處,將三角板繞點
處,將三角板繞點![]() 旋轉,三角板的兩直角邊分別交射線
旋轉,三角板的兩直角邊分別交射線![]() 、
、![]() 于
于![]() 、
、![]() 兩點.圖
兩點.圖![]() ,
,![]() ,
,![]() 是旋轉三角板得到的圖形中的
是旋轉三角板得到的圖形中的![]() 種情況.
種情況.
研究:
![]() 三角板繞點
三角板繞點![]() 旋轉,觀察線段
旋轉,觀察線段![]() 和
和![]() 之間有什么數量關系,并結合圖
之間有什么數量關系,并結合圖![]() 加以證明;
加以證明;
![]() 三角板繞點
三角板繞點![]() 旋轉,
旋轉,![]() 是否能成為等腰三角形?若能,指出所有情況(即寫出
是否能成為等腰三角形?若能,指出所有情況(即寫出![]() 為等腰三角形時
為等腰三角形時![]() 的長);若不能,請說明理由;
的長);若不能,請說明理由;
![]() 若將三角板的直角頂點放在斜邊
若將三角板的直角頂點放在斜邊![]() 上的
上的![]() 處,且
處,且![]() ,和前面一樣操作,試問線段
,和前面一樣操作,試問線段![]() 和
和![]() 之間有什么數量關系?并結合圖
之間有什么數量關系?并結合圖![]() 加以證明.
加以證明.




查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).

(1)請畫出△ABC關于y軸對稱的△DEF(其中D、E、F分別是A、B、C的對應點).
(2)直接寫出(1)中F點的坐標為 .
(3)若直線l經過點(0,﹣2)且與x軸平行,則點C關于直線l的對稱點的坐標為 .
(4)在y軸上存在一點P,使PC﹣PB最大,則點P的坐標為 .
(5)第一象限有一點M(4,2),在x軸上找一點Q使CQ+MQ最短,畫出最短路徑,保留作圖痕跡.
查看答案和解析>>
科目:初中數學 來源: 題型:
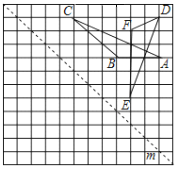
【題目】如圖,在由邊長均為1個單位長度的小正方形組成的網格中,給出了格點△ABC和△DEF(頂點 為網格線的交點),以及經過格點的直線m.
(1)畫出△ABC關于直線m對稱的△A1B1C1;
(2)將△DEF先向左平移5個單位長度,再向下平移4個單位長度,畫出平移后得到的△D1E1F1;
(3)求∠A+∠E= ________°.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在矩形![]() 中,
中,![]() ,
,![]() ,四邊形
,四邊形![]() 的三個頂點
的三個頂點![]() 、
、![]() 、
、![]() 分別在矩形
分別在矩形![]() 邊
邊![]() 、
、![]() 、
、![]() 上,
上,![]() .
.
![]() 如圖
如圖![]() ,當四邊形
,當四邊形![]() 為正方形時,求
為正方形時,求![]() 的面積;
的面積;
![]() 如圖
如圖![]() ,當四邊形
,當四邊形![]() 為菱形時,設
為菱形時,設![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并寫出函數的定義域.
的函數關系式,并寫出函數的定義域.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com