
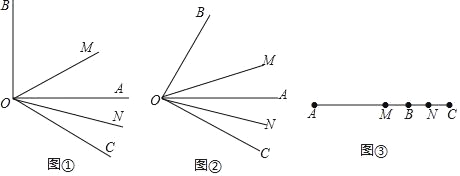
【題目】理解計算:如圖①,∠AOB=90°,∠AOC為∠AOB外的一個角,且∠AOC=30°,射線OM平分∠BOC,ON平分∠AOC.求∠MON的度數;
拓展探究:如圖②,∠AOB=α,∠AOC=β.(α,β為銳角),射線OM平分∠BOC,ON平分∠AOC.求∠MON的度數;
遷移應用:其實線段的計算與角的計算存在著緊密的聯系,如圖③線段AB=m,延長線段AB到C,使得BC=n,點M,N分別為AC,BC的中點,則MN的長為_____(直接寫出結果).
【答案】理解計算: ![]() ;拓展探究:
;拓展探究: ![]() ;遷移應用:
;遷移應用: ![]() .
.
【解析】試題分析:理解計算:根據角的平行線的特點,可以得知所分兩角相等,等于原角的一半,根據角與角之間的數量關系即可得出結論;
拓展探究:根據角的平行線的特點,可以得知所分兩角相等,等于原角的一半,根據角與角之間的數量關系即可得出結論;
遷移應用:根據上面兩題的原理,通過推導(或直接)得出結論.
試題解析:理解計算:∵∠BOC=∠AOB+∠AOC=90°+30°=120°,
射線OM平分∠BOC,
∴∠COM=![]() ∠BOC=
∠BOC=![]() ×120°=60°,
×120°=60°,
∵ON平分∠AOC,
∴∠CON=![]() ∠AOC=
∠AOC=![]() ×30°=15°,
×30°=15°,
∴∠MON=∠COM﹣∠CON=60°﹣15°=45°;
拓展探究:∵∠BOC=∠AOB+∠AOC=α+β,
∵射線OM平分∠BOC,
∴∠COM=![]() ∠BOC=
∠BOC=![]() (α+β),
(α+β),
∵ON平分∠AOC,
∴∠CON=![]() ∠AOC=
∠AOC=![]() β,
β,
∴∠MON=∠COM﹣∠CON=![]() (α+β)﹣
(α+β)﹣![]() β=
β=![]() α;
α;
遷移應用:∵AB=m,BC=n,
∴AC=AB+BC=m+n,
∵點M,N分別為AC,BC的中點,
∴CM=![]() AC=
AC=![]() (m+n),CN=
(m+n),CN=![]() BC=
BC=![]() n,
n,
∴MN=CM﹣CN=![]() m,
m,
故答案為: ![]() m.
m.


 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:初中數學 來源: 題型:
【題目】“搶紅包”是2015年春節十分火爆的一項網絡活動,某企業有4000名職工,從中隨機抽取350人,按年齡分布和“搶紅包”所持態度情況進行調查,并將調查結果繪成了條形統計圖和扇形統計圖.
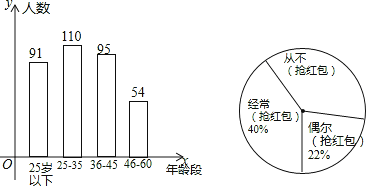
(1)這次調查中,如果職工年齡的中位數是整數,那么這個中位數所在的年齡段是哪一段?
(2)如果把對“搶紅包”所持態度中的“經常(搶紅包)”和“偶爾(搶紅包)”統稱為“參與搶紅包”,那么這次接受調查的職工中“參與搶紅包”的人數是多少?并估計該企業“從不(搶紅包)”的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
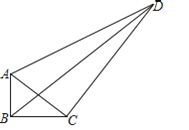
【題目】如圖,在四邊形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=![]() ,則下列結論:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四邊形ABCD的面積為31;⑤BD=2
,則下列結論:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四邊形ABCD的面積為31;⑤BD=2![]() .正確的是_______.
.正確的是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列事件中,是隨機事件的是( )
A.任意畫兩個直角三角形,這兩個三角形相似B.相似三角形的對應角相等
C.⊙O的半徑為5,OP=3,點P在⊙O外D.直徑所對的圓周角為直角
查看答案和解析>>
科目:初中數學 來源: 題型:
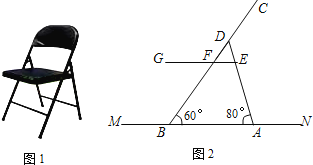
【題目】如圖1是一把折疊椅子,圖2是椅子完全打開支穩后的側面示意圖,其中AD和BC表示兩根較粗的鋼管,EG表示座板平面,EG和BC相交于點F,MN表示地面所在的直線,EG∥MN,EG距MN的高度為42cm,AB=43cm,CF=42cm,∠DBA=60°,∠DAB=80°.求兩根較粗鋼管AD和BC的長.(結果精確到0.1cm.參考數據:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin60°≈0.87,cos60°≈0.5,tan60°≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,點C、D、E三點在同一直線上,連接BD. 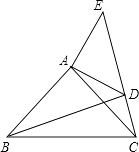
求證:
(1)△BAD≌△CAE;
(2)試猜想BD、CE有何特殊位置關系,并證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com