
【題目】如圖,在△ABC中,如果BD,CE分別是∠ABC,∠ACB的平分線且他們相交于點P,設∠A=n°.
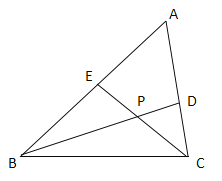
(1)求∠BPC的度數(用含n的代數式表示),寫出推理過程.
(2)當∠BPC=125°時,∠A= .
(3)當n=60°時,EB=7,BC=12,DC的長為 .
【答案】(1)∠BPC=90°+![]() n,推理過程見解析;(2)70°;(3)5.
n,推理過程見解析;(2)70°;(3)5.
【解析】
(1)根據角平分線的性質得∠ABC=2∠PBC,∠ACB=2∠PCB,再根據三角形內角和定理求得∠A=-180°+2∠BPC,即可求證∠BPC=90°+![]() n;
n;
(2)根據(1)可知∠BPC=90°+![]() n,把∠BPC=125°代入原式求出n即為∠A的度數;
n,把∠BPC=125°代入原式求出n即為∠A的度數;
(3)當n=60°時,即可求出∠BPC=120°,作輔助線在CB上截取CG=CD,可證出△CPG≌△PCD(SAS),即可得出∠DPO=∠GPC,PD=PG,再可證出△BEP≌△BGP,即可得出BE=BG,即可求出DC.
解:(1)∵DB、CE分別為∠ABC,∠ACB的平分線,
∴∠ABC=2∠PBC,∠ACB=2∠PCB.
∵∠A=180°-(∠ABC+∠ACB),
∴∠A=180°-2(∠PBC+∠PCB),
∴∠A=180°-2(180°-∠BPC),
∴∠A=-180°+2∠BPC,
∴2∠BPC=180°+∠A,
∴∠BPC=90°+![]() ∠A,
∠A,
∴∠BPC=90°+![]() n
n
(2)由(1)知∠BPC=90°+![]() ∠A
∠A
∴當∠BPC=125°時,∠A =2×(125°-90°)= 70°;
(3)在CB上截取CG=CD,連接GP,
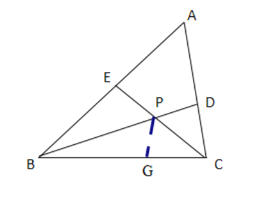
![]() CE平分
CE平分![]()
∴∠GCP=∠PCD,
在△PCD和△PCG中,
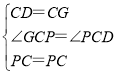
∴△PCD≌△CGP(SAS),
∴∠GPC=∠CPD,PG=PD,
由∠BPG+∠GPC=120°,
又∵∠BPG+2∠GPC=180°,
解得:∠BPG=∠GPC=∠FPC=60°
在△BEP和△BGP中,
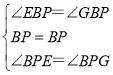
∴△BEP≌△BGP(ASA),
∴BE=BG,
∴CG=BC-BG=BC-BE=12-7=5
∴CD=CG=5.


科目:初中數學 來源: 題型:
【題目】下列說法中正確的有( )個
①對角線互相平分的四邊形是平行四邊形;②等腰梯形在同一底上的兩個內角相等;
③對角線互相垂直的四邊形是菱形;④一組鄰邊相等的矩形是正方形.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
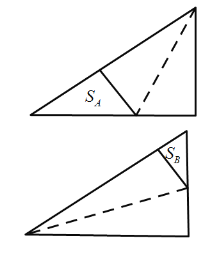
【題目】如圖是兩個全等的三角形紙片,其三邊長之比為![]() ,按圖中方法分別將其對折,使折痕(圖中虛線)過其中的一個頂點,且使該項點所在兩邊重合,記折疊后不重疊部分面積分別為
,按圖中方法分別將其對折,使折痕(圖中虛線)過其中的一個頂點,且使該項點所在兩邊重合,記折疊后不重疊部分面積分別為![]() ,已知
,已知![]() ,則紙片的面積是( )
,則紙片的面積是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應國家的號召,減少污染,某廠家生產出一種節能又環保的油電混合動力汽車,既可以用油做動力行駛,也可以用電做動力行駛.這種油電混合動力汽車從甲地行駛到乙地,若完全用油做動力行駛,費用為108元;若完全用電做動力行駛,費用為36元,已知汽車行駛中每千米用油的費用比用電的費用多0.6元.
(1)求汽車行駛中每千米用電的費用和甲、乙兩地之間的距離.
(2)若汽車從甲地到乙地采用油電混合動力行駛,且所需費用不超過60元,則至少需要用電行駛多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場服裝部為了調動營業員的積極性,決定實行目標管理,根據目標完成的情況對營業員進行適當的獎勵.為了確定一個適當的月銷售目標,商場服裝部統計了每位營業員在某月的銷售額(單位:萬元),數據如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
對這30個數據按組距3進行分組,并整理、描述和分析如下.
頻數分布表
組別 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
銷售額 |
|
|
|
|
|
|
|
頻數 | 7 | 9 | 3 |
| 2 |
| 2 |
數據分析表
平均數 | 眾數 | 中位數 |
20.3 |
| 18 |
請根據以上信息解答下列問題:
(1)填空:a= ,b= ,c= ;
(2)若將月銷售額不低于25萬元確定為銷售目標,則有 位營業員獲得獎勵;
(3)若想讓一半左右的營業員都能達到銷售目標,你認為月銷售額定為多少合適?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第一袋里有紅球和白球共![]() 個,第二袋里的紅球比白球多
個,第二袋里的紅球比白球多![]() 個,每個球除顏色外都相同.把其中一個袋子里的球倒入另一個袋里混合后.任意摸出一個球是白球的可能性和任意摸出一個紅球的可能性一樣大,問第一個袋子里的紅球和白球各幾個?
個,每個球除顏色外都相同.把其中一個袋子里的球倒入另一個袋里混合后.任意摸出一個球是白球的可能性和任意摸出一個紅球的可能性一樣大,問第一個袋子里的紅球和白球各幾個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標中,邊長為2的正方形![]() 的兩頂點
的兩頂點![]() 、
、![]() 分別在
分別在![]() 軸、
軸、![]() 軸的正半軸上,點
軸的正半軸上,點![]() 在原點.現將正方形
在原點.現將正方形![]() 繞
繞![]() 點順時針旋轉,當
點順時針旋轉,當![]() 點第一次落在直線
點第一次落在直線![]() 上時停止旋轉,旋轉過程中,
上時停止旋轉,旋轉過程中,![]() 邊交直線
邊交直線![]() 于點
于點![]() ,
,![]() 邊交
邊交![]() 軸于點
軸于點![]()

(1)求邊![]() 在旋轉過程中所掃過的面積;
在旋轉過程中所掃過的面積;
(2)旋轉過程中,當![]() 和
和![]() 平行時,求正方形
平行時,求正方形![]() 旋轉的度數;
旋轉的度數;
(3)設![]() 的周長為
的周長為![]() ,在旋轉正方形
,在旋轉正方形![]() 的過程中,
的過程中,![]() 值是否有變化?請證明你的結論.
值是否有變化?請證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1)所示,在Rt△ABC中,∠B=90°,AB=4,BC=3,將△ABC沿著AC翻折得到△ADC,如圖(2),將△ADC繞著點A旋轉到△AD′C′,連接CD′,當CD′∥AB時,四邊形ABCD的面積為_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com