
【題目】如圖,已知一條直線過(guò)點(diǎn)![]() ,且與拋物線
,且與拋物線![]() 交于
交于![]() ,
,![]() 兩點(diǎn),其中點(diǎn)
兩點(diǎn),其中點(diǎn)![]() 的橫坐標(biāo)是
的橫坐標(biāo)是![]() .
.

![]() 求這條直線的函數(shù)關(guān)系式及點(diǎn)
求這條直線的函數(shù)關(guān)系式及點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
![]() 在
在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使得
,使得![]() 是直角三角形?若存在,求出點(diǎn)
是直角三角形?若存在,求出點(diǎn)![]() 的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由.
![]() 過(guò)線段
過(guò)線段![]() 上一點(diǎn)
上一點(diǎn)![]() ,作
,作![]() 軸,交拋物線于點(diǎn)
軸,交拋物線于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在第一象限,點(diǎn)
在第一象限,點(diǎn)![]() ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)![]() 的橫坐標(biāo)為何值時(shí),
的橫坐標(biāo)為何值時(shí),![]() 的長(zhǎng)度最大?最大值是多少?
的長(zhǎng)度最大?最大值是多少?
【答案】(1) 直線![]() ,B(8,16);(2)存在,
,B(8,16);(2)存在,![]() 或
或![]() ,理由見(jiàn)解析;(3)當(dāng)
,理由見(jiàn)解析;(3)當(dāng)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() 時(shí),
時(shí),![]() 的長(zhǎng)度的最大值是
的長(zhǎng)度的最大值是![]()
【解析】
(1)首先求得點(diǎn)A的坐標(biāo),然后利用待定系數(shù)法確定直線的解析式,從而求得直線與拋物線的交點(diǎn)坐標(biāo);
(2)如圖1,過(guò)點(diǎn)B作BG∥x軸,過(guò)點(diǎn)A作AG∥y軸,交點(diǎn)為G,然后分若∠BAC=90°,則AB2+AC2=BC2;若∠ACB=90°,則AB2=AC2+BC2;若∠ABC=90°,則AB2+BC2=AC2三種情況求得m的值,從而確定點(diǎn)C的坐標(biāo);
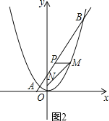
(3)設(shè)M(a,![]() a2),如圖2,設(shè)MP與y軸交于點(diǎn)Q,首先在Rt△MQN中,由勾股定理得MN=
a2),如圖2,設(shè)MP與y軸交于點(diǎn)Q,首先在Rt△MQN中,由勾股定理得MN=![]() a2+1,然后根據(jù)點(diǎn)P與點(diǎn)M縱坐標(biāo)相同得到x=
a2+1,然后根據(jù)點(diǎn)P與點(diǎn)M縱坐標(biāo)相同得到x=![]() ,從而得到MN+3PM=-
,從而得到MN+3PM=-![]() a2+3a+9,確定二次函數(shù)的最值即可.
a2+3a+9,確定二次函數(shù)的最值即可.
解:![]() ∵點(diǎn)
∵點(diǎn)![]() 是直線與拋物線的交點(diǎn),且橫坐標(biāo)為
是直線與拋物線的交點(diǎn),且橫坐標(biāo)為![]() ,
,
∴![]() ,
,![]() 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為![]() ,
,
設(shè)直線的函數(shù)關(guān)系式為![]() ,
,
將![]() ,
,![]() 代入得
代入得![]() ,
,
解得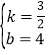 ,
,
∴直線![]() ,
,
∵直線與拋物線相交,
∴![]() ,
,
解得:![]() 或
或![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
∴點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ;
;
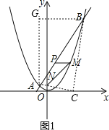
![]() 如圖
如圖![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 軸,過(guò)點(diǎn)
軸,過(guò)點(diǎn)![]() 作
作![]() 軸,交點(diǎn)為
軸,交點(diǎn)為![]() ,
,
∴![]() ,
,
∵由![]() ,
,![]() 可求得
可求得![]() .
.
設(shè)點(diǎn)![]() ,同理可得
,同理可得![]() ,
,
![]() ,
,
①若![]() ,則
,則![]() ,即
,即![]() ,
,
解得:![]() ;
;
②若![]() ,則
,則![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ;
;
③若![]() ,則
,則![]() ,即
,即![]() ,
,
解得:![]() ;
;
∴點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() ,
,![]() ,
,![]() 設(shè)
設(shè)![]() ,如圖
,如圖![]() ,設(shè)
,設(shè)![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
又∵點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 縱坐標(biāo)相同,
縱坐標(biāo)相同,
∴![]() ,
,
∴![]() ,
,
∴點(diǎn)![]() 的縱坐標(biāo)為
的縱坐標(biāo)為![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴當(dāng)![]() ,
,
又∵![]() ,
,
∴取到最小值![]() ,
,
∴當(dāng)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() 時(shí),
時(shí),![]() 的長(zhǎng)度的最大值是
的長(zhǎng)度的最大值是![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC中,AD是BC邊上的高,AE、BF分別是∠BAC、∠ABC的平分線,∠BAC=50°,∠ABC=60°,則∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,∠MON=30°,點(diǎn)A![]() 、A
、A![]() 、A
、A![]() 、A
、A![]() …在射線ON上,點(diǎn)B
…在射線ON上,點(diǎn)B![]() 、B
、B![]() 、B
、B![]() …在射線OM上,△A
…在射線OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均為等邊三角形,若OA
…均為等邊三角形,若OA![]() =1,則△A
=1,則△A![]() B
B![]() A
A![]() 的邊長(zhǎng)為( )
的邊長(zhǎng)為( )

A.64B.32C.16D.8
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的兩根,則有
的兩根,則有![]() ,
,![]() ,由上式可知,一元二次方程的兩根和、兩根積是由方程的系數(shù)確定的,我們把這個(gè)關(guān)系稱(chēng)為一元二次方程根與系數(shù)的關(guān)系.若
,由上式可知,一元二次方程的兩根和、兩根積是由方程的系數(shù)確定的,我們把這個(gè)關(guān)系稱(chēng)為一元二次方程根與系數(shù)的關(guān)系.若![]() ,
,![]() 是方程
是方程![]() 的兩根,記
的兩根,記![]() ,
,![]() ,…,
,…,![]() ,
,
![]() ________;
________;![]() ________;
________;![]() ________;
________;![]() ________;(直接寫(xiě)出結(jié)果)
________;(直接寫(xiě)出結(jié)果)
![]() 當(dāng)
當(dāng)![]() 為不小于
為不小于![]() 的整數(shù)時(shí),由
的整數(shù)時(shí),由![]() 猜想
猜想![]() ,
,![]() ,
,![]() 有何關(guān)系?
有何關(guān)系?
![]() 利用
利用![]() 中猜想求
中猜想求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在寬20米,長(zhǎng)32米的矩形耕地上,修筑同樣寬的三條路(兩條縱向,一條橫向,并且橫向與縱向互相垂直),把這塊耕地分成大小相等的六塊試驗(yàn)田,要使試驗(yàn)田的面積是570平方米,問(wèn)道路應(yīng)該多寬?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖將兩張長(zhǎng)為![]() ,寬為
,寬為![]() 的矩形紙條交叉,重疊部分是一個(gè)特殊四邊形,則這個(gè)特殊四邊形周長(zhǎng)的最小值為________.
的矩形紙條交叉,重疊部分是一個(gè)特殊四邊形,則這個(gè)特殊四邊形周長(zhǎng)的最小值為________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知正方形![]() ,點(diǎn)
,點(diǎn)![]() 為射線
為射線![]() 上的一點(diǎn)(不和點(diǎn)
上的一點(diǎn)(不和點(diǎn)![]() 、
、![]() 重合),過(guò)
重合),過(guò)![]() 作
作![]() ,且
,且![]() ,過(guò)
,過(guò)![]() 作
作![]() 交射線
交射線![]() 于
于![]() .若
.若![]() 的面積與四邊形
的面積與四邊形![]() 的面積之比為
的面積之比為![]() ,則
,則![]() ________.
________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,點(diǎn)P是AOB內(nèi)任意一點(diǎn),OP=10cm,點(diǎn)P與點(diǎn)![]() 關(guān)于射線OA對(duì)稱(chēng),點(diǎn)P與點(diǎn)
關(guān)于射線OA對(duì)稱(chēng),點(diǎn)P與點(diǎn)![]() 關(guān)于射線OB對(duì)稱(chēng),連接
關(guān)于射線OB對(duì)稱(chēng),連接![]() 交OA于點(diǎn)C,交OB于點(diǎn)D,當(dāng)△PCD的周長(zhǎng)是10cm時(shí),∠AOB的度數(shù)是______度。
交OA于點(diǎn)C,交OB于點(diǎn)D,當(dāng)△PCD的周長(zhǎng)是10cm時(shí),∠AOB的度數(shù)是______度。

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某旅行社為吸引市民組團(tuán)去天水灣風(fēng)景區(qū)旅游,推出如下收費(fèi)標(biāo)準(zhǔn):
![]() 如果人數(shù)不超過(guò)
如果人數(shù)不超過(guò)![]() 人,人均旅游費(fèi)用為
人,人均旅游費(fèi)用為![]() 元;
元;
![]() 如果人數(shù)超過(guò)
如果人數(shù)超過(guò)![]() 人,每增加
人,每增加![]() 人,人均旅游費(fèi)用降低
人,人均旅游費(fèi)用降低![]() 元,但人均旅游費(fèi)用不得低于
元,但人均旅游費(fèi)用不得低于![]() 元.
元.
某單位共付給該旅行社旅游費(fèi)用![]() 元,問(wèn):該單位這次共有多少員工去天水灣風(fēng)景區(qū)旅游?
元,問(wèn):該單位這次共有多少員工去天水灣風(fēng)景區(qū)旅游?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com