
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ�У�ֱ��![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ���c
���c![]() �S�����c(di��n)
�S�����c(di��n)![]() �����c(di��n)
�����c(di��n)![]() ����ƽ��2��(g��)��λ��������ƽ��4��(g��)��λ���õ��c(di��n)
����ƽ��2��(g��)��λ��������ƽ��4��(g��)��λ���õ��c(di��n)![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��ֱ��
��ֱ��![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ��
��
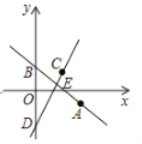
��1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��ֱ��![]() �c
�c![]() �����c(di��n)
�����c(di��n)![]() ����ֱ��
����ֱ��![]() ��ֱ��
��ֱ��![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ
��ʹ![]() �������ڣ�����c(di��n)
�������ڣ�����c(di��n)![]() ������(bi��o)���������ڣ��f(shu��)�����ɣ�
������(bi��o)���������ڣ��f(shu��)�����ɣ�
��3�������^(gu��)�c(di��n)![]() ��ֱ��
��ֱ��![]() �c����
�c����![]() �й����c(di��n)�ҝM��
�й����c(di��n)�ҝM��![]() �S
�S![]() ��������pС���O(sh��)ֱ��
��������pС���O(sh��)ֱ��![]() �c
�c![]() �S���c(di��n)�M����(bi��o)��
�S���c(di��n)�M����(bi��o)��![]() ��ֱ�ӌ���
��ֱ�ӌ���![]() ��ȡֵ����________��
��ȡֵ����________��
���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() ��
��![]() ����3��
����3��![]() ��
��![]()
��������
��1����![]() ����ֱ��
����ֱ��![]() ���������(bi��o)����(j��)�c(di��n)ƽ���c����(bi��o)��׃������c(di��n)
���������(bi��o)����(j��)�c(di��n)ƽ���c����(bi��o)��׃������c(di��n)![]() ������ֱ��
������ֱ��![]() ���ɵý�.
���ɵý�.
��2��(li��n)����ֱ������ʽ���![]() �c(di��n)����(bi��o)���M(j��n)�����
�c(di��n)����(bi��o)���M(j��n)�����![]() ����e����
����e����![]() �����ɽ��
�����ɽ��![]() ��
��![]() �S�ľ��x�������ֱ������ʽ������Ãɂ�(g��)��.
�S�ľ��x�������ֱ������ʽ������Ãɂ�(g��)��.
��3���ЃɷN��r����һ�N������ֱ��![]() �M��
�M��![]() �S
�S![]() ��������pС������(j��)һ�κ���(sh��)�����|(zh��)���ɵ�
��������pС������(j��)һ�κ���(sh��)�����|(zh��)���ɵ�![]() ����ֱ���^(gu��)�c(di��n)
����ֱ���^(gu��)�c(di��n)![]() ����
����![]() ��ԓֱ���c����
��ԓֱ���c����![]() �й����c(di��n)�������ֵ��ֱ��
�й����c(di��n)�������ֵ��ֱ��![]() �c
�c![]() �S�Ľ��c(di��n)����֮����.�ڶ��N��Сֵ��ֱ��
�S�Ľ��c(di��n)����֮����.�ڶ��N��Сֵ��ֱ��![]() �c
�c![]() �S�Ľ��c(di��n)���o(w��)���ޣ����
�S�Ľ��c(di��n)���o(w��)���ޣ����![]() �Ľ���ʽ����
�Ľ���ʽ����![]() ����֮����.
����֮����.
��1����![]() ����
����![]() ��
��![]() ���t
���t![]() ��
��
���c(di��n)![]() ����ƽ��2��(g��)��λ��������ƽ��4��(g��)��λ���õ��c(di��n)
����ƽ��2��(g��)��λ��������ƽ��4��(g��)��λ���õ��c(di��n)![]() ��
��
��![]() ��
��
���c(di��n)![]() ����
����![]() �� ��
�� ��![]() �����
�����![]() ��
��
��ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() ��
��
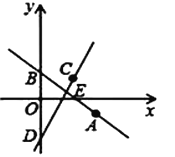
��2����![]() ��
��
���![]()
��![]()
��![]()
��![]() ����
����![]()
��![]() ����
����![]()
�C�ϣ�![]() ��
��![]()
��3����һ�N��r��
��?y��n)�ֱ��![]() �M��
�M��![]() �S
�S![]() ��������p����
��������p����![]() ��
��
ֱ��![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ����ֱ��
����ֱ��![]() �c
�c![]() �S���c(di��n)�M����(bi��o)
�S���c(di��n)�M����(bi��o)![]() ��
��
��(d��ng)ֱ��![]() �^(gu��)
�^(gu��)![]() ��
��![]() �r(sh��)���c
�r(sh��)���c![]() �S���c(di��n)�M����(bi��o)ȡ���ֵ��
�S���c(di��n)�M����(bi��o)ȡ���ֵ��
�˕r(sh��)![]() ��
��
���![]()
����ֱ������ʽ��![]() ��
��
��![]() �����
�����![]() ��
��
��ֱ��![]() �c
�c![]() �S���c(di��n)�M����(bi��o)ȡֵ������
�S���c(di��n)�M����(bi��o)ȡֵ������![]() .
.
�ڶ��N��r��
��(d��ng)ֱ��![]() �^(gu��)
�^(gu��)![]() ��
��![]() �r(sh��)���c
�r(sh��)���c![]() �S���c(di��n)�M����(bi��o)ȡ��Сֵ��
�S���c(di��n)�M����(bi��o)ȡ��Сֵ��
�˕r(sh��)![]()
���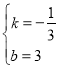
����ֱ������ʽ��![]() ��
��
��![]() �����
�����![]() ��
��
��ֱ��![]() �c
�c![]() �S���c(di��n)�M����(bi��o)ȡֵ������
�S���c(di��n)�M����(bi��o)ȡֵ������![]() .
.
�C�ϣ�ֱ��![]() �c
�c![]() �S���c(di��n)�M����(bi��o)ȡֵ������
�S���c(di��n)�M����(bi��o)ȡֵ������![]() ��
��![]() .
.


 ����˼�S��(y��u)���n��ϵ�д�
����˼�S��(y��u)���n��ϵ�д� ����ԇ��ϵ�д�
����ԇ��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
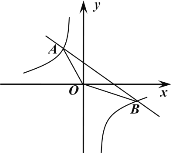
���}Ŀ����֪һ�κ���(sh��)![]() �ĈD���c����������(sh��)
�ĈD���c����������(sh��)![]() �ĈD���ཻ��A��B���c(di��n)������(bi��o)�քe��
�ĈD���ཻ��A��B���c(di��n)������(bi��o)�քe��![]() ��
��![]() ��
��
��1����ɂ�(g��)����(sh��)�Ľ���ʽ��
��2���Y(ji��)�ψD��![]() �r(sh��)��x��ȡֵ������
�r(sh��)��x��ȡֵ������
��3�����AOB����e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ھ���ABCD�У�AB��8���c(di��n)H��ֱ��AB߅�ϵ�һ��(g��)�c(di��n)���B��DH��ֱ��CB�ĸ��c(di��n)E����ֱ��AC���c(di��n)F���B��BF��
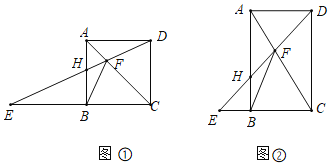
��1����D�����c(di��n)H��AB߅�ϣ�����߅��ABCD�������Σ����C����ADF�ա�ABF��
��2���ڣ�1���ėl���£�����BHF����������Σ���HF���L(zh��ng)��
��3����D������tan��ADH��![]() ���Ƿ�����c(di��n)H��ʹ�á�BHF����������Σ������ڣ���ԓ�����ε����L(zh��ng)���������ڣ�ԇ�f(shu��)�����ɣ�
���Ƿ�����c(di��n)H��ʹ�á�BHF����������Σ������ڣ���ԓ�����ε����L(zh��ng)���������ڣ�ԇ�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��![]() ���A
���A![]() ��ֱ�����c(di��n)
��ֱ�����c(di��n)![]() ���A����һ�c(di��n)��
���A����һ�c(di��n)��
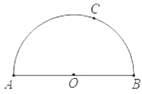
��1����![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ����A
����A![]() ���о���ֱ��
���о���ֱ��![]() ���c(di��n)
���c(di��n)![]() �����C��
�����C��![]() ��
��
��2����![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��
��![]() ��ƽ�о�����A
��ƽ�о�����A![]() ���c(di��n)
���c(di��n)![]() ����(d��ng)���c(di��n)
����(d��ng)���c(di��n)![]() ��
��![]() ��
��![]() ��
��![]() ����c(di��n)����߅�Ξ����Εr(sh��)����
����c(di��n)����߅�Ξ����Εr(sh��)����![]() ���L(zh��ng)��
���L(zh��ng)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���B������߅�ε�����(g��)��c(di��n)���õ���D��ʾ�ĈD�Σ������f(shu��)���e(cu��)�`���ǣ� ��

A. ![]() �ǵ�߅������
�ǵ�߅������
B. �B��![]() ���t
���t![]() �քeƽ��
�քeƽ��![]() ��
��![]()
C. ����(g��)�D�����S��(du��)�Q�D�Σ����������Č�(du��)�Q�D��
D. ��߅��![]() �c��߅��
�c��߅��![]() ����e���
����e���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����e�O푑�(y��ng)��ί�������ӿ콨�O(sh��)���{(l��n)ˮ�̵ؾG�������L(zh��ng)ɳ����̖(h��o)�٣�����ij�ֵ��Q���Ă��x����N�����xُ(g��u)һ�N�M(j��n)���ԷN�����˸��õ��˽��������⣬�����ˆT�ڽֵ�ݠ�^(q��)������(n��i)�S�C(j��)��ȡ�˲��־����M(j��n)�С�����ϲ�g��һ�N�䡱���{(di��o)����(d��ng)��ÿ�����x����һ�N�����������{(di��o)��Y(ji��)���������L�Ƴ���D�ɂ�(g��)�������Ľy(t��ng)Ӌ(j��)�D��

Ո(q��ng)����(j��)���o��Ϣ�������(w��n)�}��
��1���@�΅��c�{(di��o)��ľ����˔�(sh��)�飺 ��
��2��Ո(q��ng)���l�νy(t��ng)Ӌ(j��)�D�a(b��)��������
��3��Ո(q��ng)Ӌ(j��)�����νy(t��ng)Ӌ(j��)�D�С����䡱�������εĈA�ĽǶȔ�(sh��)��
��4����֪ԓ�ֵ�ݠ�^(q��)��(n��i)�F(xi��n)�о���8�f(w��n)�ˣ�Ո(q��ng)���Ӌ(j��)�@8�f(w��n)������ϲ�g���m����ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��������ABCD�У�AC=6![]() ��BD=6��E��BC߅�����c(di��n)��P��M�քe��AC��AB�ϵĄ�(d��ng)�c(di��n)���B��PE��PM���tPE+PM����Сֵ�ǣ�������
��BD=6��E��BC߅�����c(di��n)��P��M�քe��AC��AB�ϵĄ�(d��ng)�c(di��n)���B��PE��PM���tPE+PM����Сֵ�ǣ�������

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����AD��ֱ���İ�AO��(j��ng)�^(gu��)Rt��ABCб߅AB�ăɂ�(g��)���c(di��n)����ֱ��߅AC���c(di��n)E��B��E�ǰ�A�������ȷ��c(di��n)����BE���L(zh��ng)��![]() �����t�D���Ӱ���ֵ���e�飨������
�����t�D���Ӱ���ֵ���e�飨������
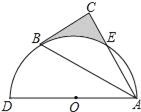
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D�٣���![]() �У�
��![]() ��
��![]() ߅��һ�c(di��n)���^(gu��)
߅��һ�c(di��n)���^(gu��)![]() �c(di��n)��
�c(di��n)��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ���B��
���B��![]() ��
��![]() ��
��![]() �����c(di��n)���B��
�����c(di��n)���B��![]() ��
��
���^����룩
��1����![]() �Ĕ�(sh��)���P(gu��n)ϵ��___________
�Ĕ�(sh��)���P(gu��n)ϵ��___________
��![]() �Ĕ�(sh��)���P(gu��n)ϵ��______________
�Ĕ�(sh��)���P(gu��n)ϵ��______________
���̽����
��2�����D����![]() �@�c(di��n)
�@�c(di��n)![]() ��r(sh��)����D(zhu��n)
��r(sh��)����D(zhu��n)![]() ����D����ʾ���t(1)�еĽY(ji��)Փ�Ƿ���Ȼ��������������Ո(q��ng)�o���C��������������Ո(q��ng)�f(shu��)�����ɣ�
����D����ʾ���t(1)�еĽY(ji��)Փ�Ƿ���Ȼ��������������Ո(q��ng)�o���C��������������Ո(q��ng)�f(shu��)�����ɣ�
����չ�w�ƣ�
��3����![]() �@�c(di��n)
�@�c(di��n)![]() ���D(zhu��n)����Ƕȣ���
���D(zhu��n)����Ƕȣ���![]() ��Ո(q��ng)ֱ�ӌ����c(di��n)
��Ո(q��ng)ֱ�ӌ����c(di��n)![]() ��ͬһֱ���ϕr(sh��)
��ͬһֱ���ϕr(sh��)![]() ���L(zh��ng)��
���L(zh��ng)��
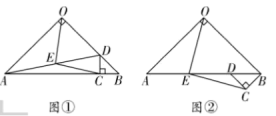
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com