
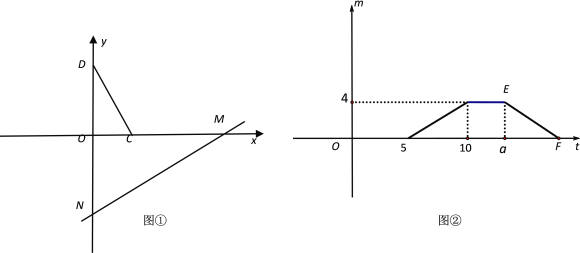
【題目】如圖①,將□ABCD置于直角坐標系中,其中BC邊在x軸上(B在C的左側),點D坐標為(0,4),直線MN:y=![]() x-6沿著x軸的負方向以每秒1個單位的長度平移,設在平移過程中該直線被□ABCD截得的線段長度為m,平移時間為t(s),m與t的函數(shù)圖像如圖②所示.
x-6沿著x軸的負方向以每秒1個單位的長度平移,設在平移過程中該直線被□ABCD截得的線段長度為m,平移時間為t(s),m與t的函數(shù)圖像如圖②所示.
(1)填空:點C的坐標為 ;在平移過程中,該直線先經過B、D中的哪一點? ;(填“B”或“D”)
(2)點B的坐標為 ,a= .
(3)求圖②中線段EF的函數(shù)關系式;
(4)t為何值時,該直線平分□ABCD的面積?
【答案】(1) (3,0),B;(2) (-2,0),![]() ;(3)EF的函數(shù)關系式y=-
;(3)EF的函數(shù)關系式y=-![]() x+
x+![]() (
(![]() ≤x≤
≤x≤![]() );(4) t=
);(4) t=![]()
【解析】試題分析: (1)根據(jù)直線解析式求出點M、N的坐標,再根據(jù)圖2判斷出CM的長,然后求出OC,從而得到點C的坐標,根據(jù)被截線段在一段時間內長度不變可以判斷出先經過點B后經過點D;
(2)根據(jù)圖2求出BM=10,再求出OB,然后寫出點B的坐標,利用勾股定理列式求出CD,再求出BC的長度,從而得到BC=CD,判斷出ABCD是菱形,根據(jù)向左平移橫坐標減表示出平移后的直線解析式,把點D的坐標代入函數(shù)解析式求出t的值即為a;
(3)根據(jù)菱形的性質寫出點A的坐標,再求出F的坐標,然后設直線EF的解析式為y=kx+b,再利用待定系數(shù)法求一次函數(shù)解析式解答;
(4)根據(jù)過平行四邊形中心的直線平分平行四邊形的面積,求出菱形的中心坐標,然后代入直線MN的解析式計算即可得解.
試題解析:
(1)令y=0,則![]() x-6=0,解得x=8,
x-6=0,解得x=8,
令x=0,則y=-6,
∴點M(8,0),N(0,-6)
∴OM=8,ON=6,
由圖2可知5秒后直線經過點C,
∴CM=5,OC=OM-CM=8-5=3,
∴C(3,0),
∵10秒~a秒被截線段長度不變,
∴先經過點B;
故答案為:(3,0);B;
(2)由圖2可知BM=10,
∴OB=BM-OM=10-8=2,
∴B(-2,0),
在Rt△OCD中,由勾股定理得,CD=![]() =5,
=5,
∴BC=CD=5,
∴ABCD是菱形.
∵設直線MN向x軸負方向平移的速度為每秒1個單位的長度,
平移后的直線解析式為y=![]() (x+t)-6,
(x+t)-6,
把點D(0,4)代入得, ![]() (0+t)-6=4,
(0+t)-6=4,
解得t=![]() ,
,
∴a=![]() .
.
故答案為:(-2,0);![]() .
.
(3)由(2)可得點E的坐標為(![]() ,4),由菱形的性質,點A(-5,4),
,4),由菱形的性質,點A(-5,4),
代入直線平移后的解析式得, ![]() (-5+t)-6=4,
(-5+t)-6=4,
解得t=![]() ,
,
∴點F(![]() ,0);
,0);
設直線EF的解析式為y=kx+b,
則 ,解得
,解得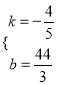 ,
,
所以線段EF的解析式為:y=![]() x+
x+![]() (
(![]() ≤x≤
≤x≤![]() );
);
(4)∵B(-2,0),D(0,4),
∴ABCD的中心坐標為(-1,2),
∵直線M平分ABCD的面積,
∴直線MN經過中心坐標,
∴![]() (-1+t)-6=2,
(-1+t)-6=2,
解得t=![]() ,
,
即t=![]() 時,該直線平分ABCD的面積.
時,該直線平分ABCD的面積.


科目:初中數(shù)學 來源: 題型:
【題目】閱讀下面材料:
小明遇到這樣一個問題:如圖1,△ABC中,AB=AC,點D在BC邊上,∠DAB=∠ABD,BE⊥AD,垂足為E,求證:BC=2AE.
小明經探究發(fā)現(xiàn),過點A作AF⊥BC,垂足為F,得到∠AFB=∠BEA,從而可證△ABF≌△BAE(如圖2),使問題得到解決.
(1)根據(jù)閱讀材料回答:△ABF與△BAE全等的條件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一個)
參考小明思考問題的方法,解答下列問題:
(2)如圖3,△ABC中,AB=AC,∠BAC=90°,D為BC的中點,E為DC的中點,點F在AC的延長線上,且∠CDF=∠EAC,若CF=2,求AB的長;
(3)如圖4,△ABC中,AB=AC,∠BAC=120°,點D、E分別在AB、AC邊上,且AD=kDB(其中0<k<![]() ),∠AED=∠BCD,求
),∠AED=∠BCD,求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】倡導健康生活,推進全民健身,某社區(qū)要購進A,B兩種型號的健身器材若干套,A,B兩種型號健身器材的購買單價分別為每套310元,460元,且每種型號健身器材必須整套購買.
(1)若購買A,B兩種型號的健身器材共50套,且恰好支出20000元,求A,B兩種型號健身器材各購買多少套?
(2)若購買A,B兩種型號的健身器材共50套,且支出不超過18000元,求A種型號健身器材至少要購買多少套?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
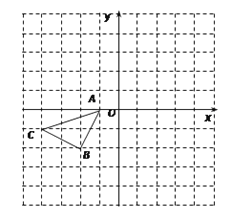
【題目】如圖所示的正方形網格中,△ABC 的頂點均在格點上,請在所給直角坐標系中按要求畫圖和解答下列問題:
(1)以A點為旋轉中心,將△ABC繞點A順時針旋轉90°得△AB1C1,畫出△AB1C1.
(2)作出△ABC關于坐標原點O成中心對稱的△A2B2C2.
(3)作出點C關于x軸的對稱點P. 若點P向右平移x個單位長度后落在△A2B2C2的內部(不含落在△A2B2C2的邊上),請直接寫出x的取值范圍.
(提醒:每個小正方形邊長為1個單位長度)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(12分)沿海某市企業(yè)計劃投入800萬元購進A、B兩種小型海水淡化設備,這兩種設備每臺的購入價、每臺設備每天可淡化的海水量及淡化率如下表:
每臺購入價(萬元) | 每臺每天可淡化海水量(立方米) | 淡化率 | |
A型 | 20 | 250 | 80% |
B型 | 25 | 400 | 75% |
(1)若該企業(yè)每天能生產9000立方米的淡化水,求購進A型、B型設備各幾臺?
(2)在(1)的條件下,已知每淡化1立方米海水所需的費用為1.5元,政府補貼0.3元.企業(yè)將淡化水以3.2元/立方米的價格出售,每年還需各項支出61萬元.按每年實際生產300天計算,該企業(yè)至少幾年后能收回成本(結果精確到個位)?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com