
| 2 | 3 |
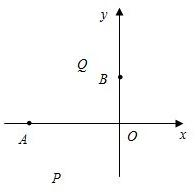 象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).
象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).| 7 |
| 2 |
| 7 |
| 2 |
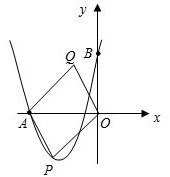 解:
解:| 2 |
| 3 |
|
|
| 2 |
| 3 |
| 14 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 14 |
| 3 |
| 7 |
| 2 |
| 2 |
| 3 |
| 14 |
| 3 |
| 7 |
| 2 |
| 2 |
| 3 |
| 14 |
| 3 |



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源:第26章《二次函數(shù)》中考題集(33):26.3 實(shí)際問(wèn)題與二次函數(shù)(解析版) 題型:解答題
 x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).
x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:第2章《二次函數(shù)》中考題集(37):2.8 二次函數(shù)的應(yīng)用(解析版) 題型:解答題
 x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).
x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).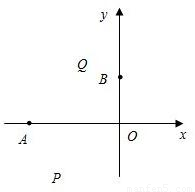
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2009年全國(guó)中考數(shù)學(xué)試題匯編《二次函數(shù)》(09)(解析版) 題型:解答題
 x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).
x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).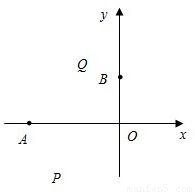
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2009年全國(guó)中考數(shù)學(xué)試題匯編《一元二次方程》(05)(解析版) 題型:解答題
 x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).
x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(t1,0),B(0,t2).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com