
【題目】已知:如圖1,二次函數y=ax2﹣2ax+c(a>0)的圖象與y軸交于點C(0,﹣4),與x軸交于點A、B兩點,點A的坐標為(4,0).

(1)求該拋物線的函數解析式;
(2)點P(t,0)是線段OB上一動點(不與O、B重合),點E是線段BC上的點,以點B、P、E為頂點的三角形與三角形ABC相似,連結CP,求△CPE的面積S與t的函數關系式;
(3)如圖2,若平行于x軸的動直線與該拋物線交于點Q,與直線AC交于點F,點D的坐標為(2,0),則存在這樣的直線,使得△ODF為等腰三角形,請直接寫出點Q坐標.
【答案】(1)y=![]() x2﹣x﹣4;(2)S=﹣
x2﹣x﹣4;(2)S=﹣![]() t2﹣
t2﹣![]() t+
t+![]() ;(3)存在這樣的直線l,使得△ODF是等腰三角形,點Q的坐標為:Q1(1+
;(3)存在這樣的直線l,使得△ODF是等腰三角形,點Q的坐標為:Q1(1+![]() ,﹣2)或Q2(1﹣
,﹣2)或Q2(1﹣![]() ,﹣2)或Q3(1+
,﹣2)或Q3(1+![]() ,﹣3)或Q4(1﹣
,﹣3)或Q4(1﹣![]() ,﹣3).
,﹣3).
【解析】
試題分析:(1)根據待定系數法,可得函數解析式;
(2)可先設P的坐標為(m,0);根據相似三角形的性質,可得S△BEP,根據S△CPE=S△BOC﹣S△BPE﹣SOPC,可得函數關系式;
(3)本題要分三種情況進行求解:①當OD=OF時,根據等腰直角三角形,可得出F的坐標應該是(2,2),根據F的縱坐標代入拋物線的解析式中即可求出Q的坐標;②當OF=DF時,根據線段垂直平分線的性質,可得OM=1,根據等腰直角三角形的性質,可得FM=AM=3,也就得出了F的縱坐標,根據①的方法求出Q的坐標;③當OD=OF時,OF=2,由于O到AC的最短距離為2![]() ,因此此種情況是不成立的,綜合上面的情況即可得出符合條件的P的坐標
,因此此種情況是不成立的,綜合上面的情況即可得出符合條件的P的坐標
解:(1)把C(0,﹣4)和A(4,0)代入y=ax2﹣2ax+c(a>0)得,
![]() ,解得
,解得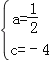
解析式為y=![]() x2﹣x﹣4;
x2﹣x﹣4;
(2)BP=t+2,OP=﹣t,S△ABC=4×6÷2=12,S△OPC=4×(﹣t)÷2=2t,
①△BPE∽△BAC,則![]() =
=![]() ,
,
則![]() =(
=(![]() )2,S△BPE=(
)2,S△BPE=(![]() )2×12=
)2×12=![]()
S△CPE=S△BOC﹣S△BPE﹣SOPC=4﹣![]() ﹣(﹣2t)=﹣
﹣(﹣2t)=﹣![]() t2+
t2+![]() t+
t+![]()
②△BEP∽△BAC,則![]() =
=![]() ,
,
則![]() =(
=(![]() )2,S△BEP=(
)2,S△BEP=(![]() )2×12=
)2×12=![]()
S△CPE=S△BOC﹣S△BPE﹣SOPC=4﹣![]() ﹣(﹣2t)=﹣
﹣(﹣2t)=﹣![]() t2﹣
t2﹣![]() t+
t+![]()
(3)存在這樣的直線,使得△ODF是等腰三角形,理由為:
在△ODF中,分三種情況考慮:
①若DO=DF,如圖1:
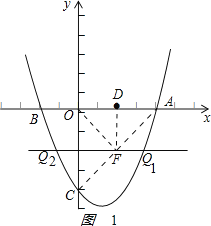 ,
,
∵A(4,0),D(2,0),
∴AD=OD=DF=2,
又在Rt△AOC中,OA=OC=4,
∴∠OAC=45°,
∴∠DFA=∠OAC=45°,
∴∠ADF=90°,
此時,點F的坐標為(2,﹣2),
由![]() x2﹣x﹣4=﹣2,
x2﹣x﹣4=﹣2,
解得:x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ,
,
此時,點P的坐標為:P(1+![]() ,﹣2)或P(1﹣
,﹣2)或P(1﹣![]() ,﹣2);
,﹣2);
②若FO=FD,過點F作FM⊥x軸于點M,如圖2:
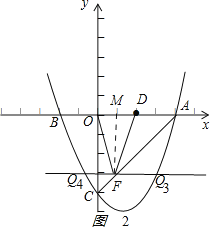 ,
,
由等腰三角形的性質得:OM=![]() OD=1,
OD=1,
∴AM=3,
∴在等腰直角△AMF中,MF=AM=3,
∴F(1,3),
由![]() x2﹣x﹣4=﹣3,
x2﹣x﹣4=﹣3,
解得:x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ,
,
此時,點P的坐標為:P(1+![]() ,﹣3)或P(1﹣
,﹣3)或P(1﹣![]() ,﹣3);
,﹣3);
③若OD=OF,
∵OA=OC=4,且∠AOC=90°,
∴AC=4 ![]() ,
,
∴點O到AC的距離為2√2,而OF=OD=2<2√2,與OF≥2√2矛盾,
所以AC上不存在點使得OF=OD=2,
此時,不存在這樣的直線l,使得△ODF是等腰三角形;
綜上所述,存在這樣的直線l,使得△ODF是等腰三角形,點Q的坐標為:Q1(1+![]() ,﹣2)或Q2(1﹣
,﹣2)或Q2(1﹣![]() ,﹣2)或Q3(1+
,﹣2)或Q3(1+![]() ,﹣3)或Q4(1﹣
,﹣3)或Q4(1﹣![]() ,﹣3).
,﹣3).


科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,對角線AC,BD相交于點O,若E,F是AC上兩動點,分別從A,C兩點以相同的速度向C、A運動,其速度為1cm/s.
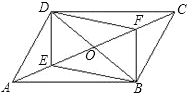
(1)當E與F不重合時,四邊形DEBF是平行四邊形嗎?說明理由;
(2)若BD=12cm,AC=16cm,當運動時間t為何值時,以D、E、B、F為頂點的四邊形是矩形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是△ABC的外接圓,AM是⊙O的直徑,過點A作AP⊥AM.

(1)求證:∠PAC=∠ABC.
(2)連接PB與AC交于點D,與⊙O交于點E,F為BD上的一點,若M為BC的中點,且∠DCF=∠P,求證:![]() =
=![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件10元,出廠價為每件12元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=﹣10x+500.
(1)李明在開始創業的第一個月將銷售單價定為20元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為w(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于25元.如果李明想要每月獲得的利潤不低于3000元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com