
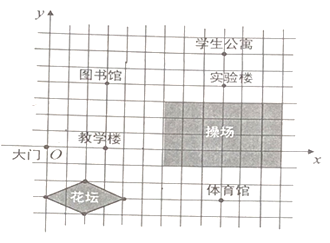
【題目】(1)如圖,是某學(xué)校的平面簡(jiǎn)圖,以學(xué)校大門位置為坐標(biāo)原點(diǎn)建立平面直角坐標(biāo)系.寫出圖中教學(xué)樓、圖書館、體育館、實(shí)驗(yàn)樓、學(xué)生公寓位置的坐標(biāo)(網(wǎng)格小正方形的邊長(zhǎng)記為1個(gè)長(zhǎng)度單位).
教學(xué)樓:_____________;
圖書館:_____________;
體育館:_____________;
實(shí)驗(yàn)樓:_____________;
學(xué)生公寓:_____________;
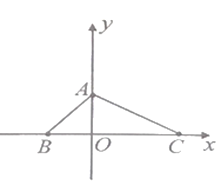
(2)點(diǎn)![]() 在坐標(biāo)系中的位置如圖所示,三角形
在坐標(biāo)系中的位置如圖所示,三角形![]() 的面積為
的面積為![]()
①三角形![]() 三個(gè)頂點(diǎn)的坐標(biāo)分別為:
三個(gè)頂點(diǎn)的坐標(biāo)分別為:![]() (____,____),
(____,____),![]() (____,_____),
(____,_____),![]() (__,__);
(__,__);
②點(diǎn)![]() 是一動(dòng)點(diǎn),若三角形
是一動(dòng)點(diǎn),若三角形![]() 面積等于三角形
面積等于三角形![]() 面積.求點(diǎn)
面積.求點(diǎn)![]() 坐標(biāo).
坐標(biāo).
【答案】(1)![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(2) ①![]()
②![]() ,
,![]()
【解析】
(1)根據(jù)建立好的平面直角坐標(biāo)系,再根據(jù)地點(diǎn)的位置寫出它們的坐標(biāo).
(2)①首先根據(jù)面積求得OA的長(zhǎng),再根據(jù)已知條件求得OB的長(zhǎng),最后求得OC的長(zhǎng),最后寫坐標(biāo)的時(shí)候注意點(diǎn)的位置,寫點(diǎn)的坐標(biāo)的時(shí)候特別注意根據(jù)點(diǎn)所在的位置來確定坐標(biāo)的符號(hào).
②根據(jù)![]() ,用含m的式子表示出
,用含m的式子表示出![]() ,由
,由![]() 即可得答案.
即可得答案.
解:(1)先在直角坐標(biāo)系中找出原點(diǎn)的位置和橫縱坐標(biāo)的方向,根據(jù)圖形得:教學(xué)樓![]() 、圖書館
、圖書館![]() 、體育館
、體育館![]() 、實(shí)驗(yàn)樓
、實(shí)驗(yàn)樓![]() 、學(xué)生公寓
、學(xué)生公寓![]()
故答案為:教學(xué)樓![]() 、圖書館
、圖書館![]() 、體育館
、體育館![]() 、實(shí)驗(yàn)樓
、實(shí)驗(yàn)樓![]() 、學(xué)生公寓
、學(xué)生公寓![]() ;
;
(2)①∵![]() ,
,![]()
∴![]()
∴![]()
∵點(diǎn)O為原點(diǎn)
∴![]()
②根據(jù)題意,可以得到三角形![]() 以AO為底邊時(shí),高可以用點(diǎn)P的橫坐標(biāo)的絕對(duì)值表示,
以AO為底邊時(shí),高可以用點(diǎn)P的橫坐標(biāo)的絕對(duì)值表示,
∴![]()
又∵![]() ,
,![]() ,
,
∴![]()
∴![]()
∴P點(diǎn)的坐標(biāo)為![]() 或
或![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(理解新知)
如圖①,已知![]() ,在
,在![]() 內(nèi)部畫射線
內(nèi)部畫射線![]() ,得到三個(gè)角,分別為
,得到三個(gè)角,分別為![]() 、
、![]() 、
、![]() ,若這三個(gè)角中有一個(gè)角是另外一個(gè)角的2倍,則稱射線
,若這三個(gè)角中有一個(gè)角是另外一個(gè)角的2倍,則稱射線![]() 為
為![]() 的“2倍角線”
的“2倍角線”
(1)角的平分線 這個(gè)角的“2倍角線”;(填“是”或“不是”)
(2)若![]() ,射線
,射線![]() 為
為![]() 的“2倍角線”,則
的“2倍角線”,則![]()
![]() ;
;
(解決問題)
如圖②,已知![]() ,射線
,射線![]() 從
從![]() 出發(fā),以每秒
出發(fā),以每秒![]() 的速度繞
的速度繞![]() 點(diǎn)逆時(shí)針旋轉(zhuǎn):射線
點(diǎn)逆時(shí)針旋轉(zhuǎn):射線![]() 從
從![]() 出發(fā),以每秒
出發(fā),以每秒![]() 的速度繞
的速度繞![]() 點(diǎn)順時(shí)針旋轉(zhuǎn),射線
點(diǎn)順時(shí)針旋轉(zhuǎn),射線![]() 、
、![]() 同時(shí)出發(fā),當(dāng)一條射線回到出發(fā)位置的時(shí)候,整個(gè)運(yùn)動(dòng)隨之停止.設(shè)運(yùn)動(dòng)的時(shí)間為
同時(shí)出發(fā),當(dāng)一條射線回到出發(fā)位置的時(shí)候,整個(gè)運(yùn)動(dòng)隨之停止.設(shè)運(yùn)動(dòng)的時(shí)間為![]() .
.
(3)當(dāng)射線![]() 、
、![]() 旋轉(zhuǎn)到同一條直線上時(shí),求
旋轉(zhuǎn)到同一條直線上時(shí),求![]() 的值;
的值;
(4)若![]() 、
、![]() 、
、![]() 三條射線中,一條射線恰好是以另外兩條射線為邊的角的“2倍角線”,直接寫出所有可能的
三條射線中,一條射線恰好是以另外兩條射線為邊的角的“2倍角線”,直接寫出所有可能的![]() 的值.(本題中所研究的角都是小于等于
的值.(本題中所研究的角都是小于等于![]() 的角.)
的角.)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直角△ABC內(nèi)接于⊙O,點(diǎn)D是直角△ABC斜邊AB上的一點(diǎn),過點(diǎn)D作AB的垂線交AC于E,過點(diǎn)C作∠ECP=∠AED,CP交DE的延長(zhǎng)線于點(diǎn)P,連結(jié)PO交⊙O于點(diǎn)F.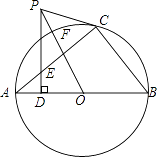
(1)求證:PC是⊙O的切線;
(2)若PC=3,PF=1,求AB的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
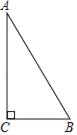
【題目】如圖,在Rt△ABC中,∠C=90°,AC=4.
(1)若BC=2,求AB的長(zhǎng);
(2)若BC=a,AB=c,求代數(shù)式(c﹣2)2﹣(a+4)2+4(c+2a+3)的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】解答下列應(yīng)用題:
⑴某房間的面積為17.6m2,房間地面恰好由110塊相同的正方形地磚鋪成,每塊地磚的邊長(zhǎng)是多少?
⑵已知第一個(gè)正方體水箱的棱長(zhǎng)是60cm,第二個(gè)正方體水箱的體積比第一個(gè)水箱的體積的3倍還多81000 cm3,則第二個(gè)水箱需要鐵皮多少平方米?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知等腰三角形ABC的底邊長(zhǎng)BC=20cm,D是AC上的一點(diǎn),且BD=16cm,CD=12cm.
(1)求證:BD⊥AC;
(2)求△ABC的面積.
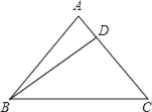
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)E為菱形ABCD的BC邊的中點(diǎn),動(dòng)點(diǎn)F在對(duì)角線AC上運(yùn)動(dòng),連接BF、EF,設(shè)AF=x,△BEF的周長(zhǎng)為y,那么能表示y與x的函數(shù)關(guān)系的大致圖象是( )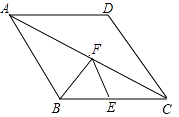
A.
B.
C.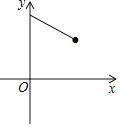
D.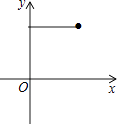
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,我們把一個(gè)半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”.已知點(diǎn)A、B、C、D分別是“果圓”與坐標(biāo)軸的交點(diǎn),拋物線的解析式為y=(x-1)2-4,AB為半圓的直徑,求這個(gè)“果圓”被y軸截得的弦CD的長(zhǎng) . 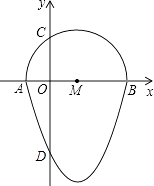
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】張大伯承包了一個(gè)四邊形的池塘,如圖所示,它的四個(gè)角A,B,C,D處均有一棵大樹,張大伯今年養(yǎng)魚喜獲豐收,明年準(zhǔn)備把池塘面積擴(kuò)大一倍,但又不想毀掉這四棵大樹,并且擴(kuò)建后的池塘呈平行四邊形形狀.張大伯這一設(shè)想是否能實(shí)現(xiàn)?請(qǐng)你幫助他解決一下,并畫出草圖.
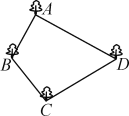
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com