
【題目】關于x的一元函數y=﹣2x+m和反比例函數y= ![]() 的圖象都經過點A(﹣2,1).
的圖象都經過點A(﹣2,1).
(1)求一次函數和反比例函數的解析式;
(2)求一次函數與反比例函數的另一個交點B的坐標;
(3)求△AOB的面積.
【答案】
(1)
解:把A(﹣2,1)代入函數關系式得到m=﹣3,n=﹣3
∴一次函數的解析式為y=﹣2x﹣3,反比例函數的解析式為y=﹣ ![]()
(2)
解:解方程組  ,得:
,得: ![]() ,
,  ,
,
∴B的坐標為( ![]() ,﹣4)
,﹣4)
(3)
解:∵一次函數的解析式為y=﹣2x﹣3,
∴y=0時,x=﹣ ![]() ,則CO=
,則CO= ![]() ,
,
∴S△AOB=S△AOC+S△BOC= ![]() =
= ![]() .
.

【解析】(1)把A的坐標代入兩個函數的解析式中就可以確定兩個函數的解析式;(2)利用兩個函數的解析式組成方程組,然后解方程組就可以確定另一個交點的坐標;(3)先確定直線與x軸的交點C的坐標,然后用面積的割補法求△AOB的面積.
【考點精析】本題主要考查了一次函數的概念和一次函數的圖象和性質的相關知識點,需要掌握一般地,如果y=kx+b(k,b是常數,k不等于0),那么y叫做x的一次函數;一次函數是直線,圖像經過仨象限;正比例函數更簡單,經過原點一直線;兩個系數k與b,作用之大莫小看,k是斜率定夾角,b與Y軸來相見,k為正來右上斜,x增減y增減;k為負來左下展,變化規律正相反;k的絕對值越大,線離橫軸就越遠才能正確解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,A(﹣2,3),B(﹣3,1),C(﹣1,2). 
(1)①將△ABC向右平移4個單位長度,畫出平移后的△A1B1C1;
②畫出△ABC關于x軸對稱的△A2B2C2;
③將△ABC繞原點O旋轉180°,畫出旋轉后的△A3B3C3;
(2)在△A1B1C1 , △A2B2C2 , △A3B3C3中,△與△成軸對稱,對稱軸是;△與△成中心對稱,對稱中心的坐標是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖,結論:①ac<0;②a﹣b+c<0;③b2﹣4ac≥0;④y隨x的增大而增大,其中正確的個數( ) 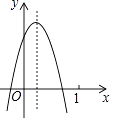
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=﹣ ![]() +bx+c的圖象經過A(2,0)、B(0,﹣6)兩點.
+bx+c的圖象經過A(2,0)、B(0,﹣6)兩點.
(1)求這個二次函數的解析式;
(2)設該二次函數的對稱軸與x軸交于點C,連接BA、BC,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB邊的垂直平分線![]() 交BC于D,AC邊的垂直平分線
交BC于D,AC邊的垂直平分線![]() 交BC于E,
交BC于E, ![]() 與
與![]() 相交于點O,△ADE的周長為6cm.
相交于點O,△ADE的周長為6cm.
(1)求BC的長;
(2)分別連結OA、OB、OC,若△OBC的周長為16cm,求OA的長;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3,AD=4,E為AB上一點,AE=1,M為射線AD上一動點,AM=a(a為大于0的常數),直線EM與直線CD交于點F,過點M作MG⊥EM,交直線BC于點G.
(1)若M為邊AD中點,求證△EFG是等腰三角形;
(2)若點G與點C重合,求線段MG的長;
(3)請用含a的代數式表示△EFG的面積S,并指出S的最小整數值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com