
【題目】受國內外復雜多變的經濟環境影響,去年1至7月,原材料價格一路攀升,長沙市某服裝廠每件衣服原材料的成本y1(元)與月份x(1≤x≤7,且x為整數)之間的函數關系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,隨著經濟環境的好轉,原材料價格的漲勢趨緩,每件原材料成本y2(元)與月份x的函數關系式為y2=x+62(8≤x≤12,且x為整數).
(1)請觀察表格中的數據,用學過的函數相關知識求y1與x的函數關系式.
(2)若去年該衣服每件的出廠價為100元,生產每件衣服的其他成本為8元,該衣服在1至7月的銷售量p1(萬件)與月份x滿足關系式p1=0.1x+1.1(1≤x≤7,且x為整數); 8至12月的銷售量p2(萬件)與月份x滿足關系式p2=﹣0.1x+3(8≤x≤12,且x為整數),該廠去年哪個月利潤最大;并求出最大利潤.
【答案】(1)![]() (1≤x≤7,且x為整數);(2)該廠去年8月利潤最大,最大利潤為48.4萬元.
(1≤x≤7,且x為整數);(2)該廠去年8月利潤最大,最大利潤為48.4萬元.
【解析】
(1)由表格中數據可猜測,y1是x的一次函數.把表格(1)中任意兩組數據代入直線解析式可得y1的解析式.
(2)分情況探討得:1≤x≤7時,利潤=P1×(售價﹣各種成本);80≤x≤12時,利潤=P2×(售價﹣各種成本);并求得相應的最大利潤即解.
解::(1)由表格中數據可猜測,y1是x的一次函數.
設![]()
則![]()
解得:![]()
∴![]() ,
,
經檢驗其它各點都符合該解析式,
∴![]() (1≤x≤7,且x為整數).
(1≤x≤7,且x為整數).
(2)設去年第x月的利潤為w萬元.
當1≤x≤7,且x為整數時,
![]()
![]()
![]()
![]()
∴當x=4時,w最大=45萬元;
當8≤x≤12,且x為整數時,
![]()
![]()
![]()
![]()
∴當x=8時,w最大=48.4萬元
∴該廠去年8月利潤最大,最大利潤為48.4萬元.


 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,A、B、C三點的坐標分別為:A(1,4)、B(0,3)、C(3,0),若P為x軸上一點,且∠BPC=2∠ACB,則點P的坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
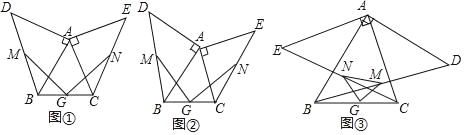
【題目】(1)操作發現:如圖①,小明畫了一個等腰三角形ABC,其中AB=AC,在△ABC的外側分別以AB,AC為腰作了兩個等腰直角三角形ABD,ACE,分別取BD,CE,BC的中點M,N,G,連接GM,GN.小明發現了:線段GM與GN的數量關系是__________;位置關系是__________.
(2)類比思考:
如圖②,小明在此基礎上進行了深入思考.把等腰三角形ABC換為一般的銳角三角形,其中AB>AC,其它條件不變,小明發現的上述結論還成立嗎?請說明理由.
(3)深入研究:
如圖③,小明在(2)的基礎上,又作了進一步的探究.向△ABC的內側分別作等腰直角三角形ABD,ACE,其它條件不變,試判斷△GMN的形狀,并給與證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊AD⊥y軸,垂足為點E,頂點A在第二象限,頂點B在y軸的正半軸上,反比例函數y=![]() (k≠0,x>0)的圖象經過頂點C、D,若點C的橫坐標為5,BE=3DE,則k的值為______.
(k≠0,x>0)的圖象經過頂點C、D,若點C的橫坐標為5,BE=3DE,則k的值為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據以下信息,解答下列問題.

(1)小華同學設乙型機器人每小時搬運xkg產品,可列方程為 .
小惠同學設甲型機器人搬運800kg所用時間為y小時,可列方程為 .
(2)請你按照(1)中小華同學的解題思路,寫出完整的解答過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平行四邊形ABCD中,對角線AC,BD交于點O,E是邊AD上的一個動點(與點A,D不重合),連接EO并延長,交BC于點F,連接BE,DF.下列說法:
① 對于任意的點E,四邊形BEDF都是平行四邊形;
② 當∠ABC>90°時,至少存在一個點E,使得四邊形BEDF是矩形;
③ 當AB<AD時,至少存在一個點E,使得是四邊形BEDF是菱形;
④ 當∠ADB=45°時,至少存在一個點E,使得是四邊形BEDF是正方形.
所有正確說法的序號是:_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】再讀教材:寬與長的比是![]() (約為0.618)的矩形叫作黃金矩形.黃金矩形給我們以協調、勻稱的美感,世界各國許多著名的建筑,為取得最佳的視覺效果,都采用了黃金矩形的設計.下面,我們用寬為2的矩形紙片折疊黃金矩形(提示:
(約為0.618)的矩形叫作黃金矩形.黃金矩形給我們以協調、勻稱的美感,世界各國許多著名的建筑,為取得最佳的視覺效果,都采用了黃金矩形的設計.下面,我們用寬為2的矩形紙片折疊黃金矩形(提示:![]() ).
).
第一步:在矩形紙片一端 ,利用圖1的方法折出一個正方形,然后把紙片展平;
第二步:如圖2,把這個正方形折成兩個相等的矩形,再把紙片展平;
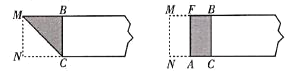
圖1 圖2
第三步:折出內側矩形的對角線![]() ,并把
,并把![]() 折到圖3中所示的
折到圖3中所示的![]() 處;
處;
第四步:展平紙片,按照所得的點![]() 折出
折出![]() ,使
,使![]() ,則圖4中就會出現黃金矩形.
,則圖4中就會出現黃金矩形.
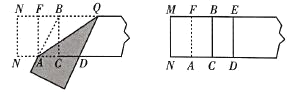
圖3 圖4
(1)在圖3中![]() _________ (保留根號);
_________ (保留根號);
(2)如圖3,則四邊形![]() 的形狀是_________;
的形狀是_________;
(3)在圖4中黃金矩形是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
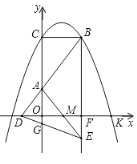
【題目】如圖,![]() 與
與![]() 軸交于點C,與
軸交于點C,與![]() 軸的正半軸交于點K,過點
軸的正半軸交于點K,過點![]() 作
作![]() 軸交拋物線于另一點B,點
軸交拋物線于另一點B,點![]() 在
在![]() 軸的負半軸上,連結
軸的負半軸上,連結![]() 交
交![]() 軸于點A,若
軸于點A,若![]() .
.
(1)用含![]() 的代數式表示
的代數式表示![]() 的長;
的長;
(2)當![]() 時,判斷點
時,判斷點![]() 是否落在拋物線上,并說明理由;
是否落在拋物線上,并說明理由;
(3)過點![]() 作
作![]() 軸交
軸交![]() 軸于點
軸于點![]() 延長
延長![]() 至
至![]() ,使得
,使得![]() 連結
連結![]() 交
交![]() 軸于點
軸于點![]() 連結AE交
連結AE交![]() 軸于點
軸于點![]() 若
若![]() 的面積與
的面積與![]() 的面積之比為
的面積之比為![]() 則求出拋物線的解析式.
則求出拋物線的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com