
 由于矩形和菱形特殊的對稱美和矩形的四個角都是直角,從而為密鋪提供了方便,因此墻磚一般設計為矩形,而且圖案以菱形居多,如圖3所示,是長為30cm,寬為20cm的一塊矩形瓷磚,E、F、G、H分別是矩形四邊的中點,陰影部分為黃色,其它部分為淡藍色,現有一面長為6m,高為3m的墻面準備貼這種瓷磚,那么:這面墻要貼的瓷磚數及全部貼滿后這面墻上最多出現的與圖3中面積相等的菱形個數分別為
由于矩形和菱形特殊的對稱美和矩形的四個角都是直角,從而為密鋪提供了方便,因此墻磚一般設計為矩形,而且圖案以菱形居多,如圖3所示,是長為30cm,寬為20cm的一塊矩形瓷磚,E、F、G、H分別是矩形四邊的中點,陰影部分為黃色,其它部分為淡藍色,現有一面長為6m,高為3m的墻面準備貼這種瓷磚,那么:這面墻要貼的瓷磚數及全部貼滿后這面墻上最多出現的與圖3中面積相等的菱形個數分別為
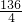 =34塊淡藍色菱形,
=34塊淡藍色菱形,

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com