
【題目】王老師為了了解所教班級學生自主學習、合作交流的具體情況,對本班部分學生進行了為期半個月的跟蹤調查,并將調查結果分成四類,A:優秀;B:良好;C:合格;D:一般;并將調查結果繪制成以下兩幅不完整的統計圖,請你根據統計圖解答下列問題:(1)本次調查中,王老師一共調查了多少名同學?
(2)將上面的條形統計圖補充完整;并求出“D”所占的圓心角的度數;
(3)從被調查的A類和D類學生中分別選取一位同學進行“一對一”互助學習,請求出所選兩位同學恰好是一位男同學和一位女同學的概率.

【答案】(1)20名;(2)補圖見解析, “D”所占的圓心角的度數為:![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)由條形統計圖與扇形統計圖,即可求得調查的總人數;(2)由(1)可 分別求得C類女生與D類男生數,補全條形統計圖;(3)首先根據題意畫出樹狀圖,然后由樹狀圖求得所有等可能的結果與所選兩位同學恰好是一位男同學和一位女同學的情況,再利用概率公式即可求得答案.
本題解析:(1)本次調查中,王老師一共調查了:(4+6)÷50%=20(名)

(2)其中C類女生有:20×25%﹣3=2(名),
D類男生有:20﹣1﹣2﹣4﹣6﹣3﹣2﹣1=1(名);
補圖如圖
“D”所占的圓心角的度數為:![]()
(3)畫樹狀圖得:
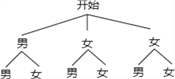
∵共有6種等可能的結果,所選兩位同學恰好是一位男同學和一位女同學的有3種情況,
∴所選兩位同學恰好是一位男同學和一位女同學的概率為:![]() .
.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案科目:初中數學 來源: 題型:
【題目】如圖,ABCD中,AB=3cm,AD=6cm,∠ADC的角平分線DE交BC于點E,交AC于點F,CG⊥DE,垂足為G,DG=![]()
![]() cm,則EF的長為( )
cm,則EF的長為( )
A.2cm
B.![]() cm
cm
C.1cm
D.![]()
![]() cm
cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知平行四邊形ABCD的對角線交于點O,點P是直線BD上任意一點(異于B、O、D三點),過P點作平行于AC的直線交直線AD于點E,交直線BA于點F,當點P在線段BD上時,易證得:AC=PE+PF(如圖①所示).當點P在線段BD的延長線上(如圖②所示)和當點P在線段DB的延長線上(如圖③所示)兩種情況時,探究線段AC、PE、PF之間的數量關系,并對圖③的結論進行證明.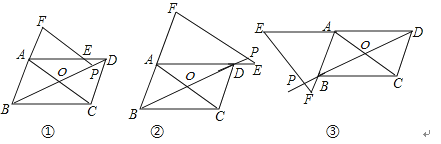
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知任意三角形ABC,
(1)如圖1,過點C作DE∥AB,求證:∠DCA=∠A;
(2)如圖1,求證:三角形ABC的三個內角(即∠A、∠B、∠ACB)之和等于180°;
(3)如圖2,求證:∠AGF=∠AEF+∠F;
(4)如圖3,AB∥CD,∠CDE=119°,GF交∠DEB的平分線EF于點F,∠AGF=150°,求∠F.
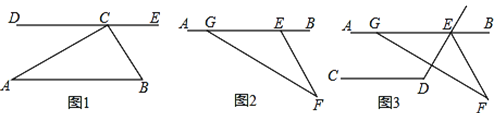
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O直徑,C、D為⊙O上不同于A、B的兩點,∠ABD=2∠BAC,連接CD.過點C作CE⊥DB,垂足為E,直線AB與CE相交于F點.
(1)求證:CF為⊙O的切線;
(2)當BF=5,![]() 時,求BD的長.
時,求BD的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com