
課本中,把長與寬之比為![]() 的矩形紙片稱為標準紙.請思考解決下列問題:
的矩形紙片稱為標準紙.請思考解決下列問題:
(1)將一張標準紙ABCD(AB<BC)對開,如圖(1)所示,所得的矩形紙片ABEF是標準紙.請給予證明.
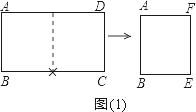
(2)在一次綜合實踐課上,小明嘗試著將矩形紙片ABCD(AB<BC)進行如下操作:
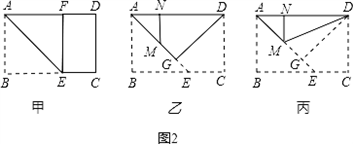
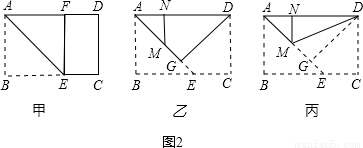
第一步:沿過A點的直線折疊,使B點落在AD邊上點F處,折痕為AE(如圖(2)甲);
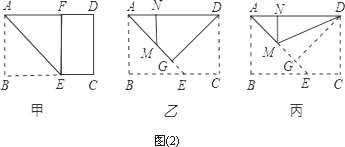
第二步:沿過D點的直線折疊,使C點落在AD邊上點N處,折痕為DG(如圖(2)乙),此時E點恰好落在AE邊上的點M處;
第三步:沿直線DM折疊(如圖(2)丙),此時點G恰好與N點重合.
請你探究:矩形紙片ABCD是否是一張標準紙?請說明理由.
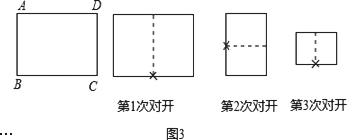
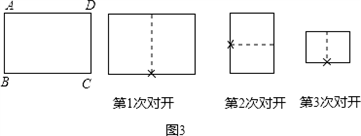
(3)不難發現:將一張標準紙按如圖(3)一次又一次對開后,所得的矩形紙片都是標準紙.現有一張標準紙ABCD,AB=1,BC=![]() ,問第5次對開后所得標準紙的周長是多少?探索直接寫出第2012次對開后所得標準紙的周長.
,問第5次對開后所得標準紙的周長是多少?探索直接寫出第2012次對開后所得標準紙的周長.
|
分析:(1)根據 (2)利用已知得出△ADG是等腰直角三角形,得出 (3)分別求出每一次對折后的周長,進而得出變化規律求出即可. 解答:解:(1)是標準紙, 理由如下: ∵矩形ABCD是標準紙, ∴ 由對開的含義知:AF= ∴ ∴矩形紙片ABEF也是標準紙. (2)是標準紙,理由如下: 設AB=CD=a,由圖形折疊可知:DN=CD=DG=a, DG⊥EM, ∵由圖形折疊可知:△ABE≌△AFE, ∴∠DAE= ∴△ADG是等腰直角三角形, ∴在Rt△ADG中,AD= ∴ ∴矩形紙片ABCD是一張標準紙; (3)對開次數: 第一次,周長為:2(1+ 第二次,周長為:2( 第三次,周長為:2( 第四次,周長為:2( 第五次,周長為:2( 第六次,周長為:2( … ∴第5次對開后所得標準紙的周長是: 第2012次對開后所得標準紙的周長為: 點評:此題主要考查了翻折變換性質以及規律性問題應用,根據已知得出對開后所得標準紙的周長變化規律是解題關鍵. |
|
考點:翻折變換(折疊問題);全等三角形的判定與性質;勾股定理;等腰直角三角形;矩形的性質;圖形的剪拼. |


 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:初中數學 來源: 題型:
| 2 |


| 2 |

查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(浙江衢州卷)數學(帶解析) 題型:解答題
課本中,把長與寬之比為 的矩形紙片稱為標準紙.請思考解決下列問題:
的矩形紙片稱為標準紙.請思考解決下列問題:
(1)將一張標準紙ABCD(AB<BC)對開,如圖1所示,所得的矩形紙片ABEF是標準紙.請給予證明.
(2)在一次綜合實踐課上,小明嘗試著將矩形紙片ABCD(AB<BC)進行如下操作:
第一步:沿過A點的直線折疊,使B點落在AD邊上點F處,折痕為AE(如圖2甲);
第二步:沿過D點的直線折疊,使C點落在AD邊上點N處,折痕為DG(如圖2乙),此時E點恰好落在AE邊上的點M處;
第三步:沿直線DM折疊(如圖2丙),此時點G恰好與N點重合.
請你探究:矩形紙片ABCD是否是一張標準紙?請說明理由.
(3)不難發現:將一張標準紙按如圖3一次又一次對開后,所得的矩形紙片都是標準紙.現有一張標準紙ABCD,AB=1,BC= ,問第5次對開后所得標準紙的周長是多少?探索直接寫出第2012次對開后所得標準紙的周長.
,問第5次對開后所得標準紙的周長是多少?探索直接寫出第2012次對開后所得標準紙的周長.
查看答案和解析>>
科目:初中數學 來源:浙江省中考真題 題型:解答題
 的矩形紙片稱為標準紙.請思考解決下列問題:
的矩形紙片稱為標準紙.請思考解決下列問題: ,問第5次對開后所得標準紙的周長是多少?探索直接寫出第2012次對開后所得標準紙的周長.…
,問第5次對開后所得標準紙的周長是多少?探索直接寫出第2012次對開后所得標準紙的周長.…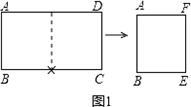
查看答案和解析>>
科目:初中數學 來源:2012年浙江省衢州市中考數學試卷(解析版) 題型:解答題
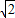 的矩形紙片稱為標準紙.請思考解決下列問題:
的矩形紙片稱為標準紙.請思考解決下列問題: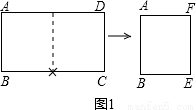
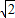 ,問第5次對開后所得標準紙的周長是多少?探索直接寫出第2012次對開后所得標準紙的周長.
,問第5次對開后所得標準紙的周長是多少?探索直接寫出第2012次對開后所得標準紙的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com