
【題目】如圖,已知:在直角![]() 中,
中,![]() ,點
,點![]() 在邊
在邊![]() 上,且
上,且![]() 如果將
如果將![]() 沿
沿![]() 所在的直線翻折,點
所在的直線翻折,點![]() 恰好落在邊
恰好落在邊![]() 上的點
上的點![]() 處,點
處,點![]() 為
為![]() 邊上的一個動點,聯結
邊上的一個動點,聯結![]() ,以
,以![]() 圓心,
圓心,![]() 為半徑作⊙
為半徑作⊙![]() ,交線段
,交線段![]() 于點
于點![]() 和點
和點![]() ,作
,作![]() 交⊙
交⊙![]() 于點
于點![]() ,
,![]() 交線段
交線段![]() 于點
于點![]() .
.
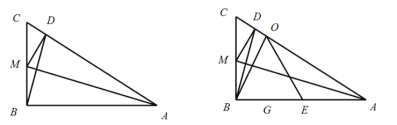
(1)求點![]() 到點
到點![]() 和直線
和直線![]() 的距離
的距離
(2)如果點![]() 平分劣弧
平分劣弧![]() ,求此時線段
,求此時線段![]() 的長度
的長度
(3)如果![]() 為等腰三角形,以
為等腰三角形,以![]() 為圓心的⊙
為圓心的⊙![]() 與此時的⊙
與此時的⊙![]() 相切,求⊙
相切,求⊙![]() 的半徑
的半徑
【答案】(1) ![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或20.
或20.
【解析】
(1)設BD與AM交于點N,那么∠BNM=90°,BN=DN,然后解直角三角形即可解答;
(2)先確定∠CAB的正弦值,再設BG=3m、OG=4m建立方程求得m;再運用解直角三角形求得BE,最后利用AE=AB-BE即可求解;
(3)先求出△AOE為等腰三角形時圓O的半徑及圓心距;然后就圓A與圓O是內切還是外切分類討論求解即可.
解:(1)如圖:設BD與AM交于點N,那么∠BNM=90°,BN=DN

∵Rt△ABM中,AB=12,BM=4,
∴tan∠2=![]() , cos∠2=
, cos∠2=![]()
∵∠1+∠BMN=90°,∠2+∠BMN=90°,
∴∠1=∠2.
∵Rt△BMN中,BM=4,
∴BN=BM·cos∠1=![]()
∴BD=2BN=![]()
如圖所示:作DH⊥AB于H,
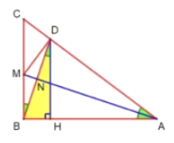
∴DH∥CB
∴∠BDH=∠MBN
∴DH=BD·cos∠BDH=![]() ×
×![]() =
=![]() ;
;
(2)∵在Rt△ADH中,DH=![]() ,AD=AB=12,
,AD=AB=12,
∴sin∠CAB=![]()
如圖所示:因為點F平分弧BE,
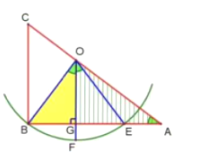
∴OF⊥BE,BG=EG
在Rt△BOG中,已知∠BOF=∠BAC,設BG=3m,OG=4m.
在Rt△AOG中,由tan∠A=![]() =
=![]() ,
,
解得m=![]()
∴AE=AB-BE=12-6m=![]() ;
;
(3)第一步,求△AOE為等腰三角形時圓O的半徑,
∵△AOE是鈍角三角形,
∴只存在EO=EA的情況。
如圖所示:作EK⊥AC于K

在Rt△AEK中,設EK=3n,則AK=4n,EA=5n.
如圖所示:作OP⊥AB于P

在Rt△AOP中,OA=2AK=8n,AP=![]() OA=
OA=![]()
∴PE=AP-AE=![]() -5n=
-5n=![]()
由AB=2PE+EA=![]() +5n=12.解得:n=
+5n=12.解得:n=![]() .
.
∴ro=OE=5n=![]() ,圓心距d=OA=
,圓心距d=OA=![]()
第二步,分兩種情況討論圓A與圓O相切.
①如圖所示,當圓A與圓O外切時,ro+ra=d,
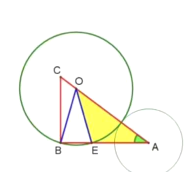
所以ra =d-ro=![]() ;
;
②如圖所示,當圓A與圓O內切時ra-ro=d

所以ra=d+ro=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】新華文具店的某種毛筆每支售價![]() 元,書法練習本每本售價
元,書法練習本每本售價![]() 元,該文具店為促銷制定了兩種優惠辦法:
元,該文具店為促銷制定了兩種優惠辦法:
甲:買一支毛筆就贈送一本書法練習本;
乙:按購買金額打九折付款.
實驗中學欲為校書法興趣小組購買這種毛筆![]() 支,書法練習本
支,書法練習本![]()
![]() 本,
本,
(1)請寫出用甲種優惠辦法實際付款金額![]() 甲(元)與
甲(元)與![]() (本)之間的函數關系式;
(本)之間的函數關系式;
(2)請寫出用乙種優惠辦法實際付款金額![]() 乙(元)與
乙(元)與![]() (本)之間的函數關系式;
(本)之間的函數關系式;
(3)若購買同樣多的書法練習本時,你會選擇哪種優惠辦法付款更省錢.
查看答案和解析>>
科目:初中數學 來源: 題型:
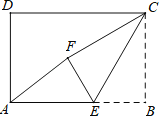
【題目】如圖,在矩形ABCD中,AB=3,CB=2,點E為線段AB上的動點,將△CBE沿CE折疊,使點B落在矩形內點F處,下列結論正確的是_____(寫出所有正確結論的序號)
①當E為線段AB中點時,AF∥CE;
②當E為線段AB中點時,AF=![]() ;
;
③當A、F、C三點共線時,AE=![]() ;
;
④當A、F、C三點共線時,△CEF≌△AEF.
查看答案和解析>>
科目:初中數學 來源: 題型:
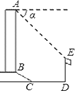
【題目】如圖,某辦公大樓正前方有一根高度是15米的旗桿ED,從辦公大樓頂端A測得旗桿頂端E的俯角α是45°,旗桿底端D到大樓前梯坎底邊的距離DC是20米,梯坎坡長BC是12米,梯坎坡度i=1:![]() ,則大樓AB的高度為________米.(精確到0.1米,參考數據:
,則大樓AB的高度為________米.(精確到0.1米,參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
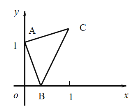
【題目】如右圖,點A的坐標為(0,1),點B是x軸正半軸上的一動點,以AB為邊作等腰直角△ABC,使∠BAC=90°,如果點B的橫坐標為x,點C的縱坐標為y,那么表示y與x的函數關系的圖像大致是( )
A.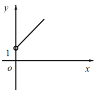 B.
B.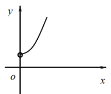
C.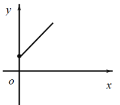 D.
D.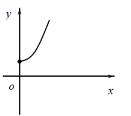
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列解題過程:
例:若代數式![]() ,求a的取值.
,求a的取值.
解:原式=![]() ,
,
當a<2時,原式=(2-a)+(4-a)=6-2a=2,解得a=2(舍去);
當2≤a<4時,原式=(a-2)+(4-a)=2=2,等式恒成立;
當a≥4時,原式=(a-2)+(a-4)=2a-6=2,解得a=4;
所以,a的取值范圍是2≤a≤4.
上述解題過程主要運用了分類討論的方法,請你根據上述理解,解答下列問題:
(1)當3≤a≤7時,化簡:![]() =_________;
=_________;
(2)請直接寫出滿足![]() =5的a的取值范圍__________;
=5的a的取值范圍__________;
(3)若![]() =6,求a的取值.
=6,求a的取值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() (點
(點![]() 在點
在點![]() 的右側),點
的右側),點![]() 為拋物線的頂點,點
為拋物線的頂點,點![]() 的縱坐標為-2.
的縱坐標為-2.
(1)如圖1,求此拋物線的解析式;
(2)如圖2,點![]() 是第一象限拋物線上一點,連接
是第一象限拋物線上一點,連接![]() ,過點
,過點![]() 作
作![]() 軸交
軸交![]() 于點
于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() 的長為
的長為![]() ,求
,求![]() 與
與![]() 的函數關系式(不要求寫出自變量
的函數關系式(不要求寫出自變量![]() 的取值范圍);
的取值范圍);
(3)如圖3,在(2)的條件下,點![]() 在
在![]() 上,且
上,且![]() ,點
,點![]() 的橫坐標大于3,連接
的橫坐標大于3,連接![]() ,
,![]() ,
,![]() ,且
,且![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人駕車分別從A、B兩地相向而行,乙出發半小時后甲出發,甲出發1.5小時后汽車出現故障,于是甲停下修車,半小時后甲修好后繼續沿原路按原速與乙相遇,相遇后甲隨即調頭以原速返回A地,乙也繼續向A地行駛,甲、乙兩車之間的距離(y/千米)與甲駕車時間x(小時)之間的關系如圖所示,當乙到達A地時,甲距離B地_____千米.
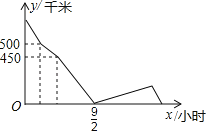
查看答案和解析>>
科目:初中數學 來源: 題型:
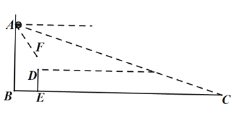
【題目】如圖,在教室前面墻壁![]() 處安裝了一個攝像頭,當恰好觀測到后面墻壁與底面交接處點
處安裝了一個攝像頭,當恰好觀測到后面墻壁與底面交接處點![]() 時,攝像頭俯角約為
時,攝像頭俯角約為![]() ,受安裝支架限制,攝像頭觀測的俯角最大約為
,受安裝支架限制,攝像頭觀測的俯角最大約為![]() ,已知攝像頭安裝點高度
,已知攝像頭安裝點高度![]() 約為
約為![]() 米,攝像頭與安裝的墻壁之間距離忽略不計,
米,攝像頭與安裝的墻壁之間距離忽略不計,
![]() 求教室的長(教室前后墻壁之間的距離
求教室的長(教室前后墻壁之間的距離![]() 的值);
的值);
![]() 若第一排桌子前邊緣與前面墻壁的距離
若第一排桌子前邊緣與前面墻壁的距離![]() 為
為![]() 米, 桌子的高度
米, 桌子的高度![]() 為
為![]() 米,那么第一排桌子是否在監控范圍內?如果不在,應該怎樣移動? (
米,那么第一排桌子是否在監控范圍內?如果不在,應該怎樣移動? (![]() ,精確到
,精確到![]() 米)
米)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com