
【題目】某學校計劃購買若干臺電腦,現從兩家商場了解到同一型號電腦每臺報價均為4000元,并且多買都有一定的優惠.甲商場的優惠條件是:第一臺按原價收費,其余每臺優惠25%;乙商場的優惠條件是:每臺優惠20%.
(1)設該學校所買的電腦臺數是x臺,選擇甲商場時,所需費用為![]() 元,選擇乙商場時,所需費用為
元,選擇乙商場時,所需費用為![]() 元,請分別寫出
元,請分別寫出![]() ,
, ![]() 與x之間的關系式;
與x之間的關系式;
(2)該學校如何根據所買電腦的臺數選擇到哪間商場購買,所需費用較少?
【答案】(1)y1=3000x+1000; y2=80%×4000x=3200x;(2)當所購買電腦超過5臺時,到甲商場購買所需費用較少;當所購買電腦少于5臺時,到乙商場買所需費用較少;即當所購買電腦為5臺時,兩家商場的所需費用相同.
【解析】試題分析:(1)商場的收費等于電腦的臺數乘以每臺的單價,則甲商場的收費y=4000+(x-1)×4000×(1-25%),乙商場的收費y=x4000×(1-20%),然后整理即可;
(2)學校選擇哪家商場購買更優惠就是比較y的大小,當y甲>y乙時,學校選擇乙家商場購買更優惠,即3000x+1000>3200x;當y甲=y乙時,學校選擇甲、乙兩家商場購買一樣優惠,即3000x+1000=3200x;當y甲<y乙時,學校選擇甲家商場購買更優惠,即3000x+1000<3200x,然后分別解不等式和方程即可得解.
試題解析:(1)y1=4000+(1-25%)(x-1)×4000=3000x+1000
y2=80%×4000x=3200x
(2)當y1<y2時,有3000x+1000<3200x,解得,x>5
即當所購買電腦超過5臺時,到甲商場購買所需費用較少;
當y1>y2時,有3000x+1000>3200x,解得x<5;
即當所購買電腦少于5臺時,到乙商場買所需費用較少;
當y1=y2時,即3000x+1000=3200x, 解得x=5.
即當所購買電腦為5臺時,兩家商場的所需費用相同.


科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件10元,出廠價為每件12元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=-10x+500.
(1)李明在開始創業的第一個月將銷售單價定為20元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為W(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于25元.如果李明想要每月獲得的利潤不低于3000元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠A=∠B,AE=BE,點D在AC邊上,∠1=∠2,AE和BD相交于點O.
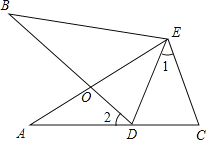
(1)求證:∠BDE=∠C;
(2)求證:△AEC≌△BED;
(3)若∠2=40°,則∠BDE=______°.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC的三邊長分別為a,b,c.
(1)若a,b,c滿足a2+b2+c2=ab+bc+ca,試判斷△ABC的形狀;
(2)若a=5,b=2,且c為整數,求△ABC的周長的最大值及最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某摩托車廠本周計劃每日生產450輛摩托車,由于工人實行輪休, 每日上班人數不一定相等,實際每日生產量與計劃量相比情況如下表: [增加的輛數為正數,減少的輛數為負數]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增減 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生產多少輛摩托車?
(2)本周總產量與計劃產量相比,是增加了還是減少了?為什么?
(3)產量最多的那天比產量最少的那天多生產多少輛?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列解題過程:
 =
= =
=![]() =
=![]() -2;
-2;
 =
= =
=![]() .
.
請回答下列問題:
(1)觀察上面的解題過程,請直接寫出式子![]() = ;
= ;
(2)觀察上面的解題過程,請直接寫出式子![]() = ;
= ;
(3)利用上面所提供的解法,請求![]() +···+
+···+![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古代阿拉伯數學家泰比特·伊本·奎拉對勾股定理進行了推廣研究:如圖(圖1中![]() 為銳角,圖2中
為銳角,圖2中![]() 為直角,圖3中
為直角,圖3中![]() 為鈍角).
為鈍角).

在△ABC的邊BC上取![]() ,
, ![]() 兩點,使
兩點,使![]() ,則
,則![]() ∽
∽![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,進而可得
,進而可得![]()
![]() ;(用
;(用![]() 表示)
表示)
若AB=4,AC=3,BC=6,則![]()
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com