
【題目】在數軸上,點A,B分別表示數a,b,且(a+12)2+|b﹣24|=0,記AB=|a﹣b|.
(1)求AB的值;
(2)如圖,點P,Q分別從點A,B同時出發沿數軸向右運動,點P的速度是每秒2個單位長度,點Q的速度是每秒4個單位長度,當BQ=2BP時,P點對應的數是多少?
(3)在(2)的條件下,點M從原點與P、Q點同時出發沿數軸向右運動,速度是每秒x個單位長度(2<x<4),若在運動過程中,2MP﹣MQ的值與運動的時間t無關,求x的值.
![]()
【答案】AB=36;(2)點P所對應的數是6;(3)x=![]()
【解析】
(1)求出a、b的值即可求出AB;
(2)設運動時間為ts,表示BQ,BP,列方程求解即可;
(3)表示出點P、M、Q所表示的數,進而表示出MP、MQ,利用2MP﹣MQ的值與運動的時間t無關,即t的系數為0,進而求出結果.
(1)∵(a+12)2+|b﹣24|=0,
∴a+12=0,b﹣24=0,
即:a=﹣12,b=24,
∴AB=|a﹣b|=|﹣12﹣24|=36.
(2)設運動的時間為ts,由BQ=2BP得:
4t=2(36﹣2t),
解得:t=9,
因此,點P所表示的數為:2×9﹣12=6,
答:點P所對應的數是6.
(3)由題意得:點P所表示的數為(﹣12+2t),點M所表示的數為xt,點Q所表示的數為(24+4t),
∴2MP﹣MQ=2[xt﹣(﹣12+2t)]﹣(24+4t﹣xt)=3xt﹣8t=(3x﹣8)t.
∵結果與t無關,
∴3x﹣8=0,
解得:x![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,點D在邊OA上,將圖中的△COD繞點O按每秒10°的速度沿順時針方向旋轉一周,在旋轉的過程中,在第________秒時,邊CD恰好與邊AB平行.

查看答案和解析>>
科目:初中數學 來源: 題型:
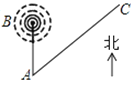
【題目】城市![]() 的正北方向
的正北方向![]() 的
的![]() 處,有一無線電信號發射塔.已知,該發射塔發射的無線電信號的有效半徑為
處,有一無線電信號發射塔.已知,該發射塔發射的無線電信號的有效半徑為![]() ,
,![]() 是一條直達
是一條直達![]() 城的公路,從
城的公路,從![]() 城發往
城發往![]() 城的班車速度為
城的班車速度為![]() .
.
(1)當班車從![]() 城出發開往
城出發開往![]() 城時,某人立即打開無線電收音機,班車行駛了
城時,某人立即打開無線電收音機,班車行駛了![]() 的時候接收信號最強.此時,班車到發射塔的距離是多少千米?(離發射塔越近,信號越強)
的時候接收信號最強.此時,班車到發射塔的距離是多少千米?(離發射塔越近,信號越強)
(2)班車從![]() 城到
城到![]() 城共行駛了
城共行駛了![]() ,請你判斷到
,請你判斷到![]() 城后還能接收到信號嗎?請說明理由.
城后還能接收到信號嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數![]() (k為常數,k≠1).
(k為常數,k≠1).
(Ⅰ)其圖象與正比例函數y=x的圖象的一個交點為P,若點P的縱坐標是2,求k的值;
(Ⅱ)若在其圖象的每一支上,y隨x的增大而減小,求k的取值范圍;
(Ⅲ)若其圖象的一支位于第二象限,在這一支上任取兩點A(x1,y1)、B(x2,y2),當y1>y2時,試比較x1與x2的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數y=![]() 與一次函數y=x+b的圖象在第一象限相交于點A(1,-k+4).
與一次函數y=x+b的圖象在第一象限相交于點A(1,-k+4).
(1)試確定這兩個函數的表達式;
(2)求出這兩個函數圖象的另一個交點B的坐標,并求△A0B的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖所示的平面直角坐標系中,
(1)畫出函數![]() 的圖象;
的圖象;
(2)填空:請寫出圖象與x軸的交點A(___,___)的坐標,與y軸交點B(___,__)的坐標;
(3)在(2)的條件下,求出△AOB的面積;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 在第二象限,其中
在第二象限,其中![]() ,
,![]() 滿足等式
滿足等式![]() ,點
,點![]() 在第一象限內,射線
在第一象限內,射線![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)當![]() 時,求
時,求![]() 點的坐標;
點的坐標;
(2)點![]() 在
在![]() 軸上從
軸上從![]() 出發以每秒1個單位長度的速度向點
出發以每秒1個單位長度的速度向點![]() 運動(到達
運動(到達![]() 點后停止運動),求當時間為
點后停止運動),求當時間為![]() 秒時(不考慮點
秒時(不考慮點![]() 與點
與點![]() 重合的情況),
重合的情況),![]() ,
,![]() ,
,![]() 的大小關系;
的大小關系;
(3)如圖,若![]() ,點
,點![]() 是射線
是射線![]() 上一動點,
上一動點,![]() ,
,![]() 的平分線交于點
的平分線交于點![]() .
.![]() 的大小是否隨點
的大小是否隨點![]() 的位置變化發生改變,若不變,請求出
的位置變化發生改變,若不變,請求出![]() 的度數;若改變,說明理由.
的度數;若改變,說明理由.



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角三角形ABC中,∠ABC=90°.

(1)先作∠ACB的平分線;設它交AB邊于點O,再以點O為圓心,OB為半徑作⊙O(尺規作圖,保留作圖痕跡,不寫作法);
(2)證明:AC是所作⊙O的切線;
(3)若BC=![]() ,∠A=30°,求△AOC的面積.
,∠A=30°,求△AOC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com