
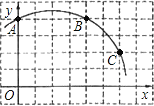
【題目】如圖,在正方形網格圖中建立一直角坐標系,一條圓弧經過網格點A、B、C,請在網格中進行下列操作:
(1)在圖中確定該圓弧所在圓的圓心D點的位置,并寫出點D點坐標為________.
(2)連接AD、CD,求⊙D的半徑及![]() 的長;
的長;
(3)有一點E(6,0),判斷點E與⊙D的位置關系.
 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
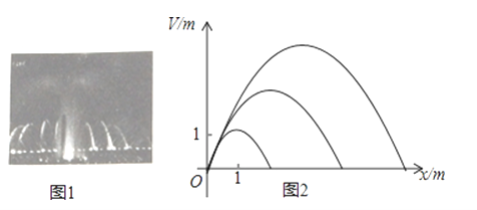
【題目】音樂噴泉(圖1)可以使噴水造型隨音樂的節奏起伏變化而變化.某種音樂噴泉形狀如拋物線,設其出水口為原點,出水口離岸邊18m,音樂變化時,拋物線的頂點在直線y=kx上變動,從而產生一組不同的拋物線(圖2),這組拋物線的統一形式為y=ax2+bx.
(1)若已知k=1,且噴出的拋物線水線最大高度達3m,求此時a、b的值;
(2)若k=1,噴出的水恰好達到岸邊,則此時噴出的拋物線水線最大高度是多少米?
(3)若k=3,a=﹣![]() ,則噴出的拋物線水線能否達到岸邊?
,則噴出的拋物線水線能否達到岸邊?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國高鐵迅猛發展,給我們的出行帶來極大的便捷,如圖1,是某種新設計動車車頭的縱截面一部分,曲線OBA是一開口向左,對稱軸正好是水平線OC的拋物線的一部分,點A、B是車頭玻璃罩的最高點和最低點,AC、BD是兩點到車廂底部的距離,OD=1.5米,BD=1.5米,AC=3米,請你利用所學的函數知識解決以下問題.
(1)為了方便研究問題,需要把曲線OBA繞點O旋轉轉化為我們熟悉的函數,請你在所給的方框內,畫出你旋轉后函數圖象的草圖,在圖中標出點O、A、B、C、D對應的位置,并求你所畫的函數的解析式.
(2)如圖2,駕駛員座椅安裝在水平線OC上一點P處,實驗表明:當PA+PB最小時,駕駛員駕駛時視野最佳,為了達到最佳視野,求OP的長.
(3)駕駛員頭頂到玻璃罩的高度至少為0.3米才感到壓抑,一個駕駛員坐下時頭頂到椅面的距離為1米,在(2)的情況下,座椅最多條件到多少時他才感到舒適?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx﹣4a經過A(﹣1,0)、C(0,4)兩點,與x軸交于另一點B.
(1)求拋物線的解析式;
(2)求拋物線的頂點坐標
(3)已知點D(m,m+1)在第一象限的拋物線上,求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
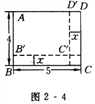
【題目】如圖2 - 4所示,長方形ABCD的長為5 cm,寬為4 cm,如果將它的長和寬都減去x(cm),那么它剩下的小長方形AB′C′D′的面積為y(cm2).
(1)寫出y與x的函數關系式;
(2)上述函數是什么函數?
(3)自變量x的取值范圍是什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
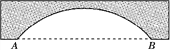
【題目】如圖,一拱形公路橋,圓弧形橋拱的水面跨度AB=80 m,橋拱到水面的最大高度為20 m.(1)求橋拱的半徑.
(2)現有一艘寬60 m,頂部截面為長方形且高出水面9 m的輪船要經過這座拱橋,這艘輪船能順利通過嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,AB=BC,∠B=∠C=90°,P是BC邊上一點,AP⊥PD,E是AB邊上一點,∠BPE=∠BAP.
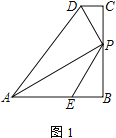
(1) 如圖1,若AE=PE,直接寫出![]() =______;
=______;
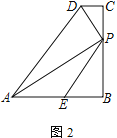
(2) 如圖2,求證:AP=PD+PE;
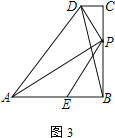
(3) 如圖3,當AE=BP時,連BD,則![]() =______,并說明理由.
=______,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用適當的方法解下列方程:
(1)(x-1)2﹣9=0;
(2)3(x+5)=(x+5)2;
(3)x2+6x-55=0;
(4)2x(x+3)-1=0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com