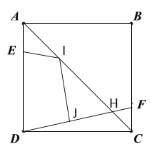
【題目】如圖，正方形
邊長為
，
，
分別為線段
，
上一點，且
，
，
與
相交于
，
為線段
上一點（不與端點重合），
為線段
上一點（不與端點重合），則
的最小值為（ ）
A.
B.
C.
D.
【答案】C
【解析】
作點E關于AC的對稱點K，EI+IJ=KI+KJ，當EJ⊥DF時
有最小值，如下圖所示，延長KJ交DC于N點，過N作NM∥AD，得到△KMN≌△FCD，再由△DJ0N∽△DCF求出J0N，最后KN減去J0N即為所求.
解：如圖，作點E關于AC的對稱點K，當EJ⊥DF時EI+IJ有最小值為KJ0，此時設KN與DF、CD的交點分別為J0和N點，過N點作MN∥AD交AB于點M.
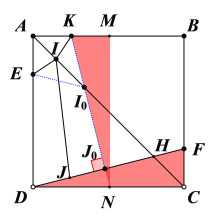
∵∠KND+∠FDC=90°，
∠DFC+∠FDC=90°
∴∠KND=∠DFC
又∵AB∥CD
∴∠MKN=∠KND=∠DFC
在△MKN和△CFD中
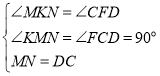，∴△MKN≌△CFD(AAS)
∴
,
又△DJ0N∽△DCF
∴
，代入數據：
，得
∴
.
故答案為：C.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】如圖所示，用一根長度為18米的原材料制作一個矩形窗戶邊框（即矩形ABFE和矩形DCFE），原材料剛好全部用完，設窗戶邊框AB長度為x米，窗戶總面積為S平方米（注：窗戶邊框粗細忽略不計）．
（1）求S與x之間的函數關系式；
（2）若窗戶邊框AB的長度不少于2米，且邊框AB的長度小于BC的長度，求此時窗戶總面積S的最大值和最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】表中所列
、
的7對值是二次函數
圖象上的點所對應的坐標，其中
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根據表中提供約信息，有以下4個判斷：①
；②
；③當
時，的值是
；④
；其中判斷正確的是（ ）
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知A(2，y1)，B(﹣3，y2)，C(﹣5，y3)三個點都在反比例函數
的圖象上，比較y1，y2，y3的大小，則下列各式正確的是( )
A.y1＜y2＜y3B.y2＜y3＜y1C.y1＜y3＜y2D.y3＜y2＜y1
查看答案和解析>>
科目：初中數學 來源： 題型：
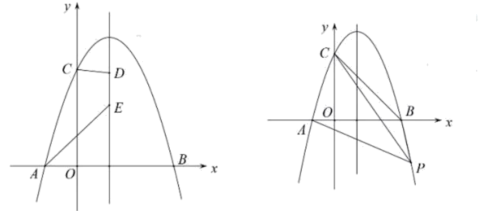
【題目】如圖所示拋物線
過點
，點
，且
（1）求拋物線的解析式及其對稱軸；
（2）點
在直線
上的兩個動點，且
，點
在點
的上方，求四邊形
的周長的最小值；
（3）點
為拋物線上一點，連接
，直線把四邊形
的面積分為3∶5兩部分，求點的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小魏探究學習函數的經驗，對函數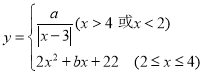
的圖像與性質進行了研究，下面是小魏的探究過程，請補充完整．
（1）下表是
與
的幾組對應值：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
請直接寫出：
_______，
______，
_______．
（2）畫出該函數圖像．
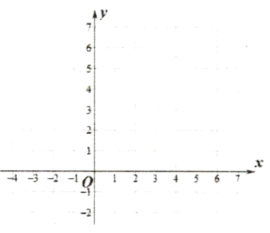
（3）寫出該函數的一條性質：_______________．
（4）一次函數
與該函數圖像至少有三個交點，則
的范圍_______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】橫、縱坐標均為整數的點稱為格點，如圖，
的三個頂點
，
，
均為格點，
上的點
也為格點，用無刻度的直尺作圖：
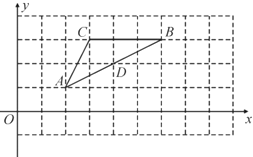
（1）將線段
繞點
順時針旋轉90°，得到線段
，寫出格點
的坐標；
（2）將線段平移至線段
，使點與點
重合，直接寫出格點
的坐標；
（3）畫出線段
關于對稱的線段
，保留作圖痕跡．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，AD平分∠BAC交⊙O于D，過D作DE⊥AC交AC延長線于點E，交AB延長線于點F．
（1）求證：EF是⊙O的切線；
（2）若DE=
，tan∠BDF=
，求DF的長．
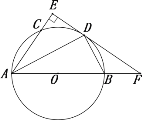
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】節假日期間向、某商場組織游戲，主持人請三位家長分別帶自己的孩于參加游戲，A、B、C分別表示一位家長，他們的孩子分別對應的是a，b，
若主持人分別從三位家長和三位孩予中各選一人參加游戲．
若已選中家長A，則恰好選中自己孩子的概率是______．
請用畫樹狀圖或列表法求出被選中的恰好是同一家庭成員的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
