
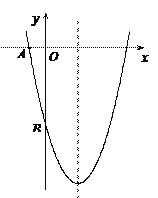
【題目】如圖,已知二次函數![]() 的圖象與坐標軸交于點A(-1, 0)和點B(0,-5).
的圖象與坐標軸交于點A(-1, 0)和點B(0,-5).
(1)求該二次函數的解析式;
(2)已知該函數圖象的對稱軸上存在一點P,使得△ABP的周長最小.請求出點P的坐標.
【答案】(1) ![]() ;(2)點P的坐標為(2,-3)
;(2)點P的坐標為(2,-3)
【解析】分析:(1)將A、B的坐標代入拋物線的解析式中,即可求得待定系數的值;
(2)設拋物線與x軸的另一交點為C,根據(1)所得的函數解析式即可求得A、B、C的坐標;在△ABP中,AB的長為定值,若三角形的周長最小,那么AP+BP的長最小;由于A、C關于拋物線的對稱軸對稱,若連接BC,那么BC與對稱軸的交點即為所求的P點,可先求出直線BC的解析式,然后聯立拋物線的對稱軸方程,即可求得P點的坐標.
詳解:(1)根據題意,聯立方程組解得 ![]() ,
,
∴二次函數的表達式為![]() ,
,
(2)令y=0,得二次函數![]() 的圖象與x軸
的圖象與x軸
的另一個交點坐標C(5, 0).
由于P是對稱軸![]() 上一點,
上一點,
連結AB,由于![]() ,
,
要使△ABP的周長最小,只要![]() 最小.
最小.
由于點A與點C關于對稱軸![]() 對稱,連結BC交對稱軸于點P,則
對稱,連結BC交對稱軸于點P,則![]() = BP+PC =BC,根據兩點之間,線段最短,可得
= BP+PC =BC,根據兩點之間,線段最短,可得![]() 的最小值為BC.
的最小值為BC.
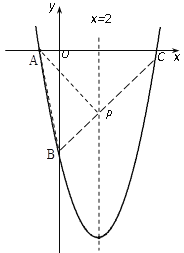
因而BC與對稱軸![]() 的交點P就是所求的點
的交點P就是所求的點
設直線BC的解析式為![]() ,根據題意,可得
,根據題意,可得![]() 解得
解得![]()
所以直線BC的解析式為![]()
因此直線BC與對稱軸![]() 的交點坐標是方程組
的交點坐標是方程組![]() 的解,解得
的解,解得![]()
所求的點P的坐標為(2,-3)


科目:初中數學 來源: 題型:
【題目】為了豐富同學的課余生活,某學校將舉行“親近大自然”戶外活動,現隨機抽取了部分學生進行主題為“你最想去的景點是________”的問卷調查,要求學生只能從“A(綠博園),B(人民公園),C(濕地公園),D(森林公園)”四個景點中選擇一項,根據調查結果,繪制了如下兩幅不完整的統計圖.
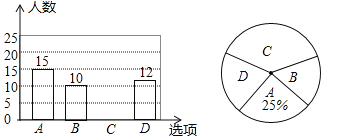
回答下列問題:
(1)本次共調查了多少名學生?
(2)補全條形統計圖;
(3)若該學校共有3 600名學生,試估計該校去濕地公園的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系內如圖1擺放,A、C兩點的橫坐標都是5,BC∥x軸.已知B點坐標為(-3,m),AB交y軸于點D,且AC=BC.
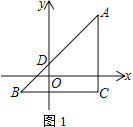
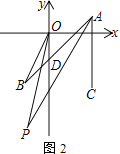
(1) 填空:BC=_____;△ABC的面積為______;用m表示點A的坐標為______.
(2) 射線BO交直線AC于點Q,若△ABQ的面積為16,試求m的值
(3) 如圖2,點D在y軸負半軸上,∠BAC的三等分線AP與∠BOD的角平分線OP交于點P,其中∠BAC=3∠BAP=45°.若∠P>2∠B,試求∠BOD的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學生的學業負擔過重會嚴重影響學生對待學習的態度.為此我市教育部門對部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:對學習很感興趣;B級:對學習較感興趣;C級:對學習不感興趣),并將調查結果繪制成圖①和圖②的統計圖(不完整).請根據圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了 名學生;
(2)將圖①補充完整;
(3)求出圖②中C級所占的圓心角的度數;
(4)根據抽樣調查結果,請你估計我市近8000名八年級學生中大約有多少名學生學習態度達標(達標包括A級和B級)?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 射線
射線![]() ,
,![]() 。
。![]() 是射線
是射線![]() 上一動點,過點
上一動點,過點![]() 作
作![]() 交射線
交射線![]() 于點
于點![]() ,連結
,連結![]() 。作
。作![]() ,交直線
,交直線![]() 于點
于點![]() ,
,![]() 平分
平分![]() 。
。

(1)若點![]() 都在點
都在點![]() 的右側。
的右側。
①求![]() 的度數;
的度數;
②若![]() ,求
,求![]() 的度數。
的度數。
(2)在點![]() 的運動過程中,是否存在這樣的情形,使
的運動過程中,是否存在這樣的情形,使![]() ,若存在,求出
,若存在,求出![]() 的度數;若不存在,請說明理由。
的度數;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】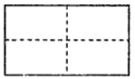
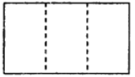
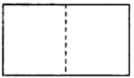
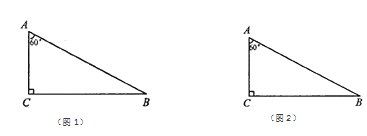
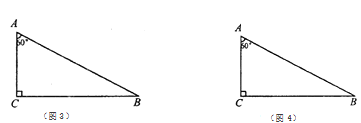
小明通過試驗發現;將一個矩形可以分別成四個全等的矩形,三個全等的矩形,二個全等的矩形(如上圖),于是他對含![]() 的直角三角形進行分別研究,發現可以分割成四個全等的三角形,三個全等的三角形.
的直角三角形進行分別研究,發現可以分割成四個全等的三角形,三個全等的三角形.
(1)請你在圖1,圖2依次畫出分割線,并簡要說明畫法;
(2)小明繼續想分割成兩個全等的三角形,發現比較困難.你能把這個直角三角形分割成兩個全等的三角形嗎?若能,畫出分割線;若不能,請說明理由.(注:備用圖不夠用可以另外畫)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新華文具用品店最近購進了一批鋼筆,進價為每支6元,為了合理定價,在銷售前4天試行機動價格,賣出時每支以10元為標準,超過10元的部分記為正,不足10元的部分記為負。文具店記錄了這四天該鋼筆的售價情況和售出情況,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支價格相對標準價格(元) | +1 | 0 | -1 | -2 |
售出支數(支) | 12 | 15 | 32 | 33 |
(1)填空:這四天中賺錢最多的是第______天,這天賺了______元錢;
(2)求新華文具用品店這四天出售這種鋼筆一共賺了多少錢;
(3)新華文具用品店準備用這四天賺的錢全部購進這種鋼筆,進價仍為每支6元為了促銷這種鋼筆,每只鋼筆的售價在10元的基礎上打九折,本次購進的這種鋼筆全部售出后共賺了多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】文美書店決定用不多于20000元購進甲乙兩種圖書共1200本進行銷售.甲、乙兩種圖書的進價分別為每本20元、14元,甲種圖書每本的售價是乙種圖書每本售價的1.4倍,若用1680元在文美書店可購買甲種圖書的本數比用1400元購買乙種圖書的本數少10本.
(1)甲乙兩種圖書的售價分別為每本多少元?
(2)書店為了讓利讀者,決定甲種圖書售價每本降低3元,乙種圖書售價每本降低2元,問書店應如何進貨才能獲得最大利潤?(購進的兩種圖書全部銷售完.)
查看答案和解析>>
科目:初中數學 來源: 題型:
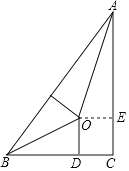
【題目】我國古代偉大的數學家劉徽將勾股形(古人稱直角三角形為勾股形)分割成一個正方形和兩對全等的直角三角形,得到一個恒等式.后人借助這種分割方法所得的圖形證明了勾股定理,如圖所示的就用了這種分割方法,若BD=2,AE=3,則正方形ODCE的邊長等于________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com