
【題目】如圖∠1=∠2,CF⊥AB,DE⊥AB,求證:FG∥BC.
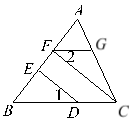
證明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
科目:初中數學 來源: 題型:
【題目】閱讀理解:課外興趣小組活動時,老師提出了如下問題:
如圖1,△ABC中,若AB=5,AC=3,求BC邊上的中線AD的取值范圍.
小明在組內經過合作交流,得到了如下的解決方法:延長AD到E,使得DE=AD,再連接BE(或將△ACD繞點D逆時針旋轉180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三邊關系可得2<AE<8,則1<AD<4.
感悟:解題時,條件中若出現“中點”“中線”字樣,可以考慮構造以中點為對稱中心的中心對稱圖形,把分散的已知條件和所求證的結論集中到同一個三角形中.
(1)問題解決:受到(1)的啟發,請你證明下面命題:如圖2,在△ABC中,D是BC邊上的中點,DE⊥DF,DE交AB于點E,DF交AC于點F,連接EF.
①求證:BE+CF>EF;②若∠A=90°,探索線段BE、CF、EF之間的等量關系,并加以證明;
(2)問題拓展:如圖3,在平行四邊形ABCD中,AD=2AB,F是AD的中點,作CE⊥AB,垂足E在線段AB上,聯結EF、CF,那么下列結論①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序號).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序號).


圖1 圖2 圖3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市中小學全面開展“陽光體育”活動,某校在大課間中開設了A:體操,B:跑操,C:舞蹈,D:健美操四項活動,為了解學生最喜歡哪一項活動,隨機抽取了部分學生進行調查,并將調查結果繪制成了如下兩幅不完整的統計圖,請根據統計圖回答下列問題:
(1)這次被調查的學生共有 人.
(2)請將統計圖2補充完整.
(3)統計圖1中B項目對應的扇形的圓心角是 度.
(4)已知該校共有學生3600人,請根據調查結果估計該校喜歡健美操的學生人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,O是AC上一動點(不與點A、C重合),過O作直線MN∥BC,設MN交∠BCA的平分線于點E,交∠BCA的外角平分線于點F.
(1)OE與OF相等嗎?證明你的結論;
(2)試確定點O的位置,使四邊形AECF是矩形,并加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1)所示,E為矩形ABCD的邊AD上一點,動點P,Q同時從點B出發,點P沿折線BE﹣ED﹣DC運動到點C時停止,點Q沿BC運動到點C時停止,它們運動的速度都是1cm/秒.設P、Q同時出發t秒時,△BPQ的面積為ycm2 . 已知y與t的函數關系圖象如圖(2)(曲線OM為拋物線的一部分),則下列結論:①AD=BE=5;② ![]() ;③當0<t≤5時,
;③當0<t≤5時, ![]() ;④當
;④當 ![]() 秒時,△ABE∽△QBP;其中正確的結論是( )
秒時,△ABE∽△QBP;其中正確的結論是( )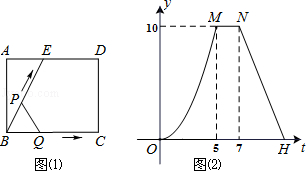
A.①②③
B.②③
C.①③④
D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年3月,某市教育主管部門在初中生中開展了“文明禮儀知識競賽”活動,活動結束后,隨機抽取了部分同學的成績(x均為整數,總分100分),繪制了如下尚不完整的統計圖表.
調查結果統計表
組別 | 成績分組(單位:分) | 頻數 | 頻率 |
A | 80≤x<85 | 50 | 0.1 |
B | 85≤x<90 | 75 | |
C | 90≤x<95 | 150 | c |
D | 95≤x≤100 | a | |
合計 | b | 1 |
根據以上信息解答下列問題:
(1)統計表中,a=_____,b=_____,c=_____;
(2)扇形統計圖中,m的值為_____,“C”所對應的圓心角的度數是_____;
(3)若參加本次競賽的同學共有5000人,請你估計成績在95分及以上的學生大約有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知經過原點的拋物線y=ax2+bx+c(a≠0)的對稱軸是直線x=﹣1,下列結論中: ①ab>0,②a+b+c>0,③當﹣2<x<0時,y<0.
正確的個數是( )
A.0個
B.1個
C.2個
D.3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,D是BA延長線上一點,E是AC的中點. 
(1)利用尺規作出∠DAC的平分線AM,連接BE并延長交AM于點F,(要求在圖中標明相應字母,保留作圖痕跡,不寫作法);
(2)試判斷AF與BC有怎樣的位置關系與數量關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com