
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 在
在![]() 上,過點
上,過點![]() 作
作![]() 的切線
的切線![]() .
.

![]() 求證:
求證:![]() ;
;
![]() 延長
延長![]() 到
到![]() ,使
,使![]() ,連接
,連接![]() 與
與![]() 交于點
交于點![]() ,若
,若![]() 的半徑為
的半徑為![]() ,
,![]() ,求
,求![]() 的外接圓的半徑.
的外接圓的半徑.
【答案】(1)詳見解析;(2)![]() 的外接圓的半徑為:
的外接圓的半徑為:![]() .
.
【解析】
(1)連接OC,由∠ABC+∠BAC=90°及CM是⊙O的切線得出∠ACM+∠ACO=90°,再利用∠BAC=∠ACO,即可得出結論,(2)證明△AEC是直角三角形,即可得△AEC的外接圓的直徑是AC,再證得△ABC∽△CDE,根據相似三角形的性質求得BC的長,利用勾股定理求出AC的長,即可求得△ACE的外接圓的半徑.
![]() 證明:如圖,連接
證明:如圖,連接![]() ,
,
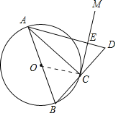
∵![]() 為
為![]() 的直徑,
的直徑,
∴![]() ,
,
∴![]() ,
,
又∵![]() 是
是![]() 的切線,
的切線,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 解:∵
解:∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,
是直角三角形,
∴![]() 的外接圓的直徑是
的外接圓的直徑是![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() 的半徑為
的半徑為![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的外接圓的半徑為
的外接圓的半徑為![]() 的一半,故
的一半,故![]() 的外接圓的半徑為:
的外接圓的半徑為:![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線BD經過坐標原點,矩形的邊分別平行于坐標軸,點C在反比例函數![]() 的圖象上.若點A的坐標為(-2,-2),則k的值為 。
的圖象上.若點A的坐標為(-2,-2),則k的值為 。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一條河的北岸有兩個目標M、N,現在位于它的對岸設定兩個觀測點A、B.已知AB∥MN,在A點測得∠MAB=60°,在B點測得∠MBA=45°,AB=600米.
(1)求點M到AB的距離;(結果保留根號)
(2)在B點又測得∠NBA=53°,求MN的長.(結果精確到1米)
(參考數據:![]() ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應“綠色出行”的號召,小王上班由自駕車改為乘坐公交車.已知小王家距離上班地點![]() ,他乘坐公交車平均每小時行駛的路程比他自駕車平均每小時行駛的路程的
,他乘坐公交車平均每小時行駛的路程比他自駕車平均每小時行駛的路程的![]() 倍還多
倍還多![]() .他從家出發到上班地點,乘公交車所用的時間是自駕車所用時間的
.他從家出發到上班地點,乘公交車所用的時間是自駕車所用時間的![]() .
.
(1)小王用自駕車上班平均每小時行駛多少千米?
(2)上周五,小王上班時先步行了![]() ,然后乘公交車前往,共用
,然后乘公交車前往,共用![]() 小時到達.求他步行的速度.
小時到達.求他步行的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知等腰直角三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 分別為邊
分別為邊![]() 、
、![]() 、
、![]() 的中點,點
的中點,點![]() 為斜邊
為斜邊![]() 所在直線上一動點,且三角形
所在直線上一動點,且三角形![]() 為等腰直角三角形(
為等腰直角三角形(![]() ,
,![]() 、
、![]() 、
、![]() 呈逆時針).
呈逆時針).
![]() 如圖
如圖![]() 點
點![]() 在邊
在邊![]() 上,判斷
上,判斷![]() 和
和![]() 的數量和位置關系,請直接寫出你的結論.
的數量和位置關系,請直接寫出你的結論.
![]() 如圖
如圖![]() 點
點![]() 在
在![]() 點左側時;如圖
點左側時;如圖![]() ,點
,點![]() 在
在![]() 點右側.其他條件不變,
點右側.其他條件不變,![]() 中結論是否仍然成立,并選擇圖
中結論是否仍然成立,并選擇圖![]() 或圖
或圖![]() 的一種情況來說明理由.
的一種情況來說明理由.
![]() 在圖
在圖![]() 中若
中若![]() ,連接
,連接![]() ,請猜測
,請猜測![]() 與
與![]() 的數量關系,即
的數量關系,即![]() ________
________![]() .(用含
.(用含![]() 的三角函數的式子表示)
的三角函數的式子表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點C為線段AB上一點,分別以AC、BC為邊在線段AB同側作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE=α,直線AE與BD交于點F.
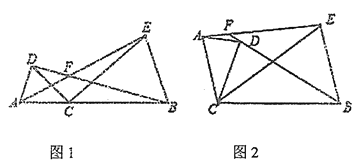
(1)如圖1所示,
①求證AE= BD
②求∠AFB (用含α的代數式表示)
(2)將圖1中的△ACD繞點C順時針旋轉某個角度(交點F至少在BD、AE中的一條線段上),得到如圖2所示的圖形,若∠AFB= 150°,請直接寫出此時對應的α的大小(不用證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y1=kx+1(k<0)與直線y2=mx(m>0)的交點坐標為(![]() ,
,![]() m),則不等式組mx﹣2<kx+1<mx的解集為( )
m),則不等式組mx﹣2<kx+1<mx的解集為( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】太極揉推器是一種常見的健身器材.基本結構包括支架和轉盤,數學興趣小組的同學對某太極揉推器的部分數據進行了測量:如圖,立柱AB的長為125cm,支架CD、CE的長分別為60cm、40cm,支點C到立柱頂點B的距離為25cm.支架CD,CE與立柱AB的夾角∠BCD=∠BCE=45°,轉盤的直徑FG=MN=60cm,D,E分別是FG,MN的中點,且CD⊥FG,CE⊥MN,則兩個轉盤的最低點F,N距離地面的高度差為_____cm.(結果保留根號)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com