
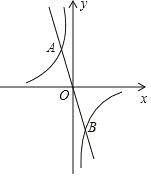
【題目】如圖,在平面直角坐標系 xOy 中,已知正比例函數 y1=﹣2x 的圖象與反比例函數 y2=![]() 的圖象交于 A(﹣1,a),B 兩點.
的圖象交于 A(﹣1,a),B 兩點.
(1)求出反比例函數的解析式及點 B 的坐標;
(2)觀察圖象,請直接寫出滿足 y≤2 的取值范圍;
(3)點 P 是第四象限內反比例函數的圖象上一點,若△POB 的面積為 1,請直接寫出點 P的橫坐標.
【答案】(1)y=﹣![]() ,B(1,﹣2);(2)x
,B(1,﹣2);(2)x![]() ﹣1 或 x>0;(3)
﹣1 或 x>0;(3)![]() .
.
【解析】
(1)已知點A的坐標代入正比例函數可求出a,再把點A坐標代入可求出反比例函數解析式;又因為正比例函數和反比例函數交點是A、B,可知A、B兩點關于原點對稱從而可求出B點坐標
(2)觀察圖像即可得出
(3)根據題意補全圖形把三角形的面積轉換成梯形的面積然后根據已知求解一元二次方程,把不符合實際情況的根舍掉即可得出答案。
(1)把 A(﹣1,a)代入 y=﹣2x,可得 a=2,
∴A(﹣1,2),
把 A(﹣1,2)代入 y=![]() ,可得 k=﹣2,
,可得 k=﹣2,
∴反比例函數的表達式為 y=﹣![]() ,
,
∵點 B 與點 A 關于原點對稱,
∴B(1,﹣2).
(2)∵A(﹣1,2),
∴y≤2 的取值范圍是 x![]() ﹣1 或 x>0;
﹣1 或 x>0;
(3)作 BM⊥x 軸于 M,PN⊥x 軸于 N,
∵S 梯形 MBPN=S△POB=1,
設 P(m,﹣![]() ),則
),則![]() ×(2+
×(2+![]() )(m﹣1)=1 或
)(m﹣1)=1 或![]() ×(2+
×(2+![]() )(1﹣m)=1整理得,m2﹣m﹣1=0 或 m2+m+1=0,
)(1﹣m)=1整理得,m2﹣m﹣1=0 或 m2+m+1=0,
解得 m=![]()
∴P 點的橫坐標![]()


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:初中數學 來源: 題型:
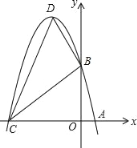
【題目】已知:m,n是方程x2﹣6x+5=0的兩個實數根,且m<n,拋物線y=﹣x2+bx+c的圖象經過點A(m,0),B(0,n).
(1)求這個拋物線的解析式;
(2)設(1)中的拋物線與x軸的另一交點為C,拋物線的頂點為D,試求出點C,D的坐標和△BCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 和
和![]() ,以下說法:
,以下說法:
①它們的圖象都是開口向上;②它們的對稱軸都是y軸,頂點坐標都是原點(0,0);③當x>0時,它們的函數y都是隨x的增大而增大;④它們的開口的大小是一樣的.
其中正確的說法有_______個.
查看答案和解析>>
科目:初中數學 來源: 題型:
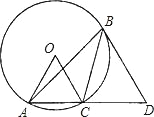
【題目】如圖,在⊙O 的內接△ABC 中,∠ABC=30°,AC 的延長線與過點 B 的⊙O 的切線相交于點 D,若⊙O 的半徑 OC=1,BD∥OC,則 CD 的長為( )
A. 1+![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
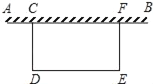
【題目】如圖,某校廣場有一段25米長的舊圍欄,現打算利用該圍欄的一部分(或全部)為一邊,圍成一塊100平方米的長方形草坪(如圖CDEF,CD<CF)已知整修舊圍欄的價格是每米1.75元,建新圍欄的價格是4.5元.若CF=x米,計劃修建費為y元.
(1)求y與x的函數關系式,并指出x的取值范圍;
(2)若計劃修建費為150元,能否完成該草坪圍欄的修建任務?若能完成,請算出利用舊圍欄多少米;若不能完成,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知⊙O的半徑為10,圓心O到弦AB的距離為5,則弦AB所對的圓周角的度數是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com