
【題目】如圖,將△ABC沿著過AB中點D的直線折疊,使點A落在BC邊上的A1處,稱為第1次操作,折痕DE到BC的距離記為h1 , 還原紙片后,再將△ADE沿著過AD中點D1的直線折疊,使點A落在DE邊上的A2處,稱為第2次操作,折痕D1E1到BC的距離記為h2;按上述方法不斷操作下去…,經過第2017次操作后得到的折痕D2016E2016 , 到BC的距離記為h2017;若h1=1,則h2017的值為 . 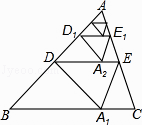
【答案】2﹣ ![]()
【解析】解:如圖,連接AA1 . 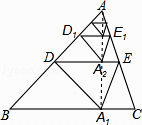
由折疊的性質可得:AA1⊥DE,DA=DA1 ,
又∵D是AB中點,
∴DA=DB,
∴DB=DA1 ,
∴∠BA1D=∠B,
∴∠ADA1=2∠B,
又∵∠ADA1=2∠ADE,
∴∠ADE=∠B,
∴DE//BC,
∴AA1⊥BC,
∴AA1=2,
∴h1=2﹣1=1,
同理,h2=2﹣ ![]() ,h3=2﹣
,h3=2﹣ ![]() ×
× ![]() =2﹣
=2﹣ ![]() ,…
,…
∴經過第n次操作后得到的折痕Dn﹣1En﹣1到BC的距離hn=2﹣ ![]() .
.
∴h2017=2﹣ ![]() .
.
所以答案是:2﹣ ![]() .
.
【考點精析】解答此題的關鍵在于理解翻折變換(折疊問題)的相關知識,掌握折疊是一種對稱變換,它屬于軸對稱,對稱軸是對應點的連線的垂直平分線,折疊前后圖形的形狀和大小不變,位置變化,對應邊和角相等.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】我國宋朝數學家楊輝在他的著作![]() 詳解九章算法
詳解九章算法![]() 中提出“楊輝三角”
中提出“楊輝三角”![]() 如圖
如圖![]() ,此圖揭示了
,此圖揭示了![]() 為非負整數
為非負整數![]() 展開式的項數及各項系數的有關規律.
展開式的項數及各項系數的有關規律.
例如:![]() ,它只有一項,系數為1;系數和為1;
,它只有一項,系數為1;系數和為1;
![]() ,它有兩項,系數分別為1,1,系數和為2;
,它有兩項,系數分別為1,1,系數和為2;
![]() ,它有三項,系數分別為1,2,1,系數和為4;
,它有三項,系數分別為1,2,1,系數和為4;
![]() ,它有四項,系數分別為1,3,3,1,系數和為8;
,它有四項,系數分別為1,3,3,1,系數和為8;![]() ,
,
則![]() 的展開式共有______項,系數和為______.
的展開式共有______項,系數和為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形紙片ABCD中折疊,使頂點B落在邊AD的E點上折痕FG交BC于G,交AB于F,若∠AEF=20°,則∠FGB的度數為( ) 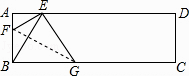
A.25°
B.30°
C.35°
D.40°
查看答案和解析>>
科目:初中數學 來源: 題型:
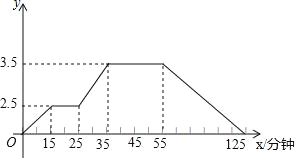
【題目】如圖所示的圖象反映的過程是:小強星期天從家跑步去體育場,在那里鍛煉了一會兒后又走到文具店去買筆,然后步行回家,其中x表示時間,y表示小強離家的距離,根據圖象回答下列問題.
(1)體育場離小強家有多遠?小強從家到體育場用了多長時間?
(2)體育場距文具店多遠?
(3)小強在文具店逗留了多長時間?
(4)小強從文具店回家的平均速度是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛貨車從百貨大樓出發負責送貨,向東走了 5 千米到達小明家,繼續向東走了 1.5 千米到達小紅家,然后向西走了 9.5 千米到達小剛家,最后返回百貨大樓.
![]()
(1)以百貨大樓為原點,向東為正方向,1 個單位長度表示 1 千米,請你在數軸上標出小明、小紅、小剛家的位置.(小明家用點 A 表示,小紅家用點 B 表示,小剛家用點 C 表示)
(2)小明家與小剛家相距多遠?
(3)若貨車每千米耗油 0.6 升,那么這輛貨車此次送貨共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形AOCB的邊長為4,反比例函數y= ![]() (k≠0,且k為常數)的圖象過點E,且S△AOE=3S△OBE .
(k≠0,且k為常數)的圖象過點E,且S△AOE=3S△OBE . 
(1)求k的值;
(2)反比例函數圖象與線段BC交于點D,直線y= ![]() x+b過點D與線段AB交于點F,延長OF交反比例函數y=
x+b過點D與線段AB交于點F,延長OF交反比例函數y= ![]() (x<0)的圖象于點N,求N點坐標.
(x<0)的圖象于點N,求N點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的兩條角平分線BD、CE交于O,且∠A=60°,則下列結論中不正確的是( )

A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
查看答案和解析>>
科目:初中數學 來源: 題型:
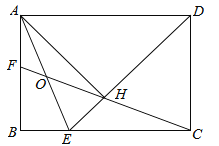
【題目】(3分)如圖,在矩形ABCD中,BC=![]() AB,∠ADC的平分線交邊BC于點E,AH⊥DE于點H,連接CH并延長交邊AB于點F,連接AE交CF于點O.給出下列命題:
AB,∠ADC的平分線交邊BC于點E,AH⊥DE于點H,連接CH并延長交邊AB于點F,連接AE交CF于點O.給出下列命題:
①∠AEB=∠AEH;②DH=![]() EH;③HO=
EH;③HO=![]() AE;④BC﹣BF=
AE;④BC﹣BF=![]() EH.
EH.
其中正確命題的序號是 (填上所有正確命題的序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
①最大的負整數是﹣1;②數軸上表示數2 和﹣2的點到原點的距離相等;③當a≤0時,|a|=﹣a成立;④a的倒數是![]() ;⑤(﹣2)2 和﹣22相等.
;⑤(﹣2)2 和﹣22相等.
A. 2 個 B. 3 個 C. 4 個 D. 5 個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com