
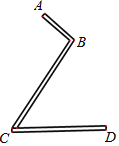
【題目】現有一個“![]() ”型的工件(工件厚度忽略不計),如圖示,其中
”型的工件(工件厚度忽略不計),如圖示,其中![]() 為20
為20![]() ,
,![]() 為60
為60![]() ,
,![]() ,
,![]() ,求該工件如圖擺放時的高度(即
,求該工件如圖擺放時的高度(即![]() 到
到![]() 的距離).
的距離).
(結果精確到0.1![]() ,參考數據:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
,參考數據:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
【答案】58.8cm
【解析】
過B作BE⊥CD,垂足為E,過A作AF⊥BE,垂足為F,根據Rt△BCE的三角函數得出BE的長度,然后根據Rt△ABF的三角形你是得出BF的長度,最后根據EF=BE+BF得出答案.
過B作BE⊥CD,垂足為E,過A作AF⊥BE,垂足為F,
在Rt△BCE中, ∵sin∠BCE =![]() , ∴BE=BC·sin∠BCE≈60×0.766 ≈45.96
, ∴BE=BC·sin∠BCE≈60×0.766 ≈45.96
又∵∠ABC=90°∴∠ABF=50°;在Rt△ABF中cos∠ABF =![]()
∴BF=AB·cos∠ABF≈20×0.463 ≈12.86
∴EF=BE+BF=45.96+12.86=58.82≈58.8(cm).
答:工件擺放時的高度是58.8cm


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
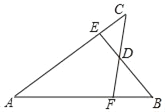
【題目】如圖,已知AB=AC,AE=AF,BE與CF交于點D,則對于下列結論:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分線上.其中正確的是( )
A. ① B. ② C. ①和② D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為滿足市場需求,新生活超市在端午節前夕購進價格為3元/個的某品牌粽子,根據市場預測,該品牌粽子每個售價4元時,每天能出售500個,并且售價每上漲0.1元,其銷售量將減少10個,為了維護消費者利益,物價部門規定,該品牌粽子售價不能超過進價的200%,請你利用所學知識幫助超市給該品牌粽子定價,使超市每天的銷售利潤為800元.
查看答案和解析>>
科目:初中數學 來源: 題型:
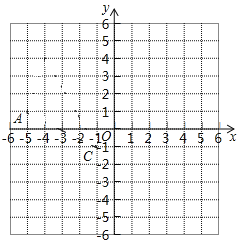
【題目】如圖,在平面直角坐標系xOy中,△ABC三個頂點都在格點上,且坐標分別為A(-2,4),B(-2,1),C(-5,2).
(1)在坐標系中,標出三個頂點坐標,并畫出△ABC;
(2)作出△ABC關于x軸對稱的△A1B1C1;
(3)將![]() 的三個頂點的橫坐標和縱坐標同時乘以
的三個頂點的橫坐標和縱坐標同時乘以![]() ,得到對應的點
,得到對應的點![]() 、
、![]() 、
、![]() ,畫出
,畫出![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
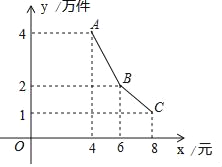
【題目】為了支持大學生創業,某市政府出臺了一項優惠政策:提供10萬元的無息創業貸款.小王利用這筆貸款,注冊了一家淘寶網店,招收5名員工,銷售一種火爆的電子產品,并約定用該網店經營的利潤,逐月償還這筆無息貸款.已知該產品的成本為每件4元,員工每人每月的工資為4千元,該網店還需每月支付其它費用1萬元.該產品每月銷售量y(萬件)與銷售單價x(元)萬件之間的函數關系如圖所示.
(1)求該網店每月利潤w(萬元)與銷售單價x(元)之間的函數表達式;
(2)小王自網店開業起,最快在第幾個月可還清10萬元的無息貸款?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是二次函數y=ax2+bx+c的部分x,y的對應值:
x | … | -1 | - | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| -1 | - | -2 | - | -1 |
| 2 | … |
(1)此二次函數圖象的頂點坐標是 ;
(2)當拋物線y=ax2+bx+c的頂點在直線y=x+n的下方時,n的取值范圍是 。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】金瑞公司決定從廠家購進甲、乙兩種不同型號的顯示器共50臺,購進顯示器的總金額不超過77000元,已知甲、乙型號的顯示器價格分別為1000元/臺、2000元/臺.
(1)求金瑞公司至少購進甲型顯示器多少臺?
(2)若甲型顯示器的臺數不超過乙型顯示器的臺數,則有哪些購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為8,在各邊上順次截取AE=BF=CG=DH=5,則四邊形EFGH的面積是( )
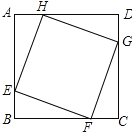
A. 30 B. 34 C. 36 D. 40
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com