
【題目】如圖,已知在矩形ABCD中,AB=a,BC=b,點E是線段AD邊上的任意一點(不含端點A、D),連結BE、CE.
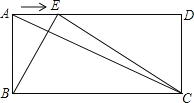
(1)若a=5,sin∠ACB=![]() ,求b.
,求b.
(2)若a=5,b=10當BE⊥AC時,求出此時AE的長.
(3)設AE=x,試探索點E在線段AD上運動過程中,使得△ABE與△BCE相似時,求a、b應滿足什么條件,并求出此時x的值.
【答案】(1)b=12;(2)![]() ;(3)當a、b滿足條件b=2a時△BAE∽△CEB,此時
;(3)當a、b滿足條件b=2a時△BAE∽△CEB,此時![]() (或x=a);當a、b滿足條件b>2a時△BAE∽△CEB,此時
(或x=a);當a、b滿足條件b>2a時△BAE∽△CEB,此時![]() .
.
【解析】
試題分析:(1)①在矩形ABCD中,得到∠ABC=90°,解直角三角形即可得到結果;
(2)由BE⊥A,得到∠2+∠3=90°,由于∠1+∠3=90°,等量代換得到∠1=∠2,推出△AEB∽△BAC,得到比例式,即可得到結論;
(3)點E在線段AD上的任一點,且不與A、D重合,當△ABE與△BCE相似時,則∠BEC=90°當△BAE∽△CEB(如圖2),∠1=∠BCE,又BC∥AD,由平行線的性質得到∠2=∠BCE,推出△BAE∽△EDC,得到比例式,進而可得得到一元二次方程x2﹣bx+a2=0,根據方程根的情況,得到結論.
解:(1)
∵四邊形ABCD是矩形,
∴∠ABC=90°,
∵AB=a=5,sin∠ACB=![]() ,
,
∴![]() ,
,
∴AC=13,
∴BC=![]() =12,
=12,
∴b=12;
(2)如圖1,
∵BE⊥AC,
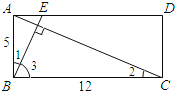
∴∠2+∠3=90°,
又∠1+∠3=90°,
∴∠1=∠2,
又∠BAE=∠ABC=90°,
∴△AEB∽△BAC,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
(3)∵點E在線段AD上的任一點,且不與A、D重合,
∴當△ABE與△BCE相似時,則∠BEC=90°
所以當△BAE∽△CEB(如圖2)
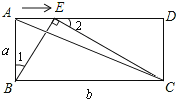
則∠1=∠BCE,
又BC∥AD,
∴∠2=∠BCE,
∴∠1=∠2,
又∠BAE=∠EDC=90°,
∴△BAE∽△EDC,
∴![]() ,
,
即![]() ,
,
∴x2﹣bx+a2=0,
即![]() ,
,
當b2﹣4a2≥0,
∵a>0,b>0,
∴b≥2a,
即b≥2a時,![]() ,
,
綜上所述:當a、b滿足條件b=2a時△BAE∽△CEB,此時![]() (或x=a);
(或x=a);
當a、b滿足條件b>2a時△BAE∽△CEB,此時![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,某市對位于筆直公路上的兩個小區A、B的供水路線進行優化改造,測得供水站M在小區A的南偏東60°方向,在小區B的西南方向,小區B到供水站M的距離為300米,
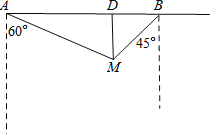
(1)求供水站M到公路AB的垂直距離MD的長度.
(2)求小區A到供水站M的距離.(結果可保留根號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com