Question

【題目】如圖，拋物線經過、兩點，與軸交于另一點．

求此拋物線的解析式；

已知點在第四象限的拋物線上，求點關于直線對稱的點的坐標．

在的條件下，連接，問在軸上是否存在點，使？若存在，請求出點的坐標；若不存在，請說明理由．

Answer 1

【答案】 ；點關于直線對稱的點；存在．，或．

【解析】

（1）將A（-1，0）、C（0，-3）兩點坐標代入拋物線y=ax2+bx-3a中，列方程組求a、b的值即可；

（2）將點D（m，-m-1）代入（1）中的拋物線解析式，求m的值，再根據對稱性求點D關于直線BC對稱的點D'的坐標；

（3）分兩種情形①過點C作CP∥BD，交x軸于P，則∠PCB=∠CBD，②連接BD′，過點C作CP′∥BD′，交x軸于P′，

分別求出直線CP和直線CP′的解析式即可解決問題．

將、代入拋物線中，

得，

解得，

∴；

將點代入中，得

，

解得或，

∵點在第四象限，

∴，

∵直線解析式為，

∴，，，

∴點關于直線對稱的點；

存在．

過點作軸，垂足為，交直線于點（如圖），

∵，

∴，

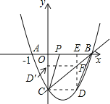
又∵軸，四邊形為平行四邊形，

∴，

∴，

設與相交于點，

易求解析式為：，

由，得到關于的方程，解方程后，得；

于是，點坐標為：；

于是解析式為：，

令方程中，，則，

所以，點坐標為：，

∴，或．