Question

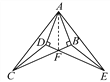
【題目】如圖，∠ABC＝∠ADE＝90°，AD＝AB，AC＝AE，BC與DE相交于點F，連接CD、EB.

(1)圖中共有幾對全等三角形，請你一一列舉；

(2)求證：CF＝EF.

Answer 1

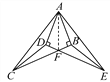
【答案】（1）有三對全等三角形，具體見解析；（2）證明見解析.

【解析】試題分析：（1）根據全等三角形的判定，結合圖形得出即可；

（2）連接AF，根據HL證Rt△ABC≌Rt△ADE推出BC=DE，根據HL推出△ADF≌△ABF，推出DF=BF，利用線段的差即可得.

試題解析：(1) 圖中有3對全等三角形有Rt△ABC≌Rt△ADE，△ACD≌△AEB，△CDF≌△EBF；

(2)連接AF，

∵∠ABC＝∠ADE＝90°，AB＝AD，AC＝AE，

∴Rt△ABC≌Rt△ADE(HL)，

∴BC＝DE，

在Rt△ABF和Rt△ADF中，AB＝AD，AF＝AF，

∴Rt△ABF≌Rt△ADF(HL)，

∴BF＝DF，

∴BC－BF＝DE－DF，

即CF＝EF.