
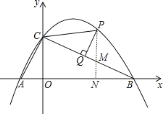
【題目】如圖,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸相交于點
軸相交于點![]() 、
、![]() ,與
,與![]() 軸相交于點
軸相交于點![]() .
.
![]() 求該函數(shù)的表達式;
求該函數(shù)的表達式;
![]() 點
點![]() 為該函數(shù)在第一象限內(nèi)的圖象上一點,過點
為該函數(shù)在第一象限內(nèi)的圖象上一點,過點![]() 作
作![]() ,垂足為點
,垂足為點![]() ,連接
,連接![]() .
.
①求線段![]() 的最大值;
的最大值;
②若以點![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,求點
相似,求點![]() 的坐標.
的坐標.

【答案】![]()
![]() ;
;![]() 滿足條件的
滿足條件的![]() 點坐標為
點坐標為![]() 或
或![]() .
.
【解析】
(1)根據(jù)待定系數(shù)法求函數(shù)關(guān)系式;(2)根據(jù)相似三角形列出比例式表示PQ值.
![]() 拋物線解析式為
拋物線解析式為![]() ,
,
即![]() ,
,
則![]() ,解得
,解得![]() ,
,
所以拋物線解析式為![]() ;
;
![]() ①作
①作![]() 軸于
軸于![]() ,交
,交![]() 于
于![]() ,如圖,
,如圖,
![]() ,
,
當(dāng)![]() 時,
時,![]() ,則
,則![]() ,
,
設(shè)直線![]() 的解析式為
的解析式為![]() ,
,
把![]() ,
,![]() 得
得![]() ,解得
,解得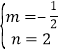 ,
,
∴直線![]() 的解析式為
的解析式為![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴當(dāng)![]() 時,線段
時,線段![]() 的最大值為
的最大值為![]() ;
;
②當(dāng)![]() 時,
時,![]() ,
,
此時![]() ,點
,點![]() 和點
和點![]() 關(guān)于直線
關(guān)于直線![]() 對稱,
對稱,
∴此時![]() 點坐標為
點坐標為![]() ;
;
當(dāng)![]() 時,
時,![]() ,
,
∵![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() 為等腰三角形,
為等腰三角形,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
此時![]() 點坐標為
點坐標為![]() ,
,
綜上所述,滿足條件的![]() 點坐標為
點坐標為![]() 或
或![]() .
.


 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案 小題狂做系列答案
小題狂做系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,小華剪了兩條寬為1的紙條,交叉疊放在一起,且它們較小的交角為60°,則它們重疊部分的面積為( )

A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
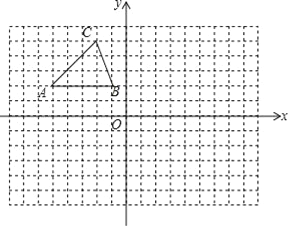
【題目】在如圖的方格中,每個小正方形的邊長都為1,△ABC的頂點均在格點上.在建立平面直角坐標系后,點B的坐標為(﹣1,2).
(1)把△ABC向下平移8個單位后得到對應(yīng)的△A1B1C1,畫出△A1B1C1;
(2)畫出與△A1B1C1關(guān)于y軸對稱的△A2B2C2;
(3)若點P(a,b)是△ABC邊上任意一點,P2是△A2B2C2邊上與P對應(yīng)的點,寫出P2的坐標為 ;
(4)試在y軸上找一點Q(在圖中標出來),使得點Q到B2、C2兩點的距離之和最小,并求出QB2+QC2的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在長度為1個單位長度的小正方形組成的長方形中,點A,B,C在小正方形的頂點上.
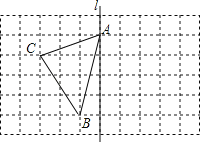
(1)在圖中畫出與△ABC關(guān)于直線l成軸對稱的△AB′C′;
(2)計算△ABC的面積;
(3)在直線l上找一點P,使PB+PC的長最短.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,三孔橋橫截面的三個孔都呈拋物線形,左右兩個拋物線形是全等的.正常水位時,大孔水面寬度為![]() ,頂點距水面
,頂點距水面![]() ,小孔頂點距水面
,小孔頂點距水面![]() .當(dāng)水位上漲剛好淹沒小孔時,大孔的水面寬度為________
.當(dāng)水位上漲剛好淹沒小孔時,大孔的水面寬度為________![]() .
.
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知O為坐標原點,四邊形OABC為長方形,A(10,0),C(0,4),點D是OA的中點,點P在BC上運動.
(1)當(dāng)△ODP是等腰三角形時,請直接寫出點P的坐標;
(2)求△ODP周長的最小值.(要有適當(dāng)?shù)膱D形和說明過程)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,CE⊥AD于點E,且CB=CE,點F為CD邊上的一點,CB=CF,連接BF交CE于點G.
(1)若∠D=60°,CF=2![]() ,求CG的長度;
,求CG的長度;
(2)求證:AB=ED+CG.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,DE是邊AB的垂直平分線,交AB于E、交AC于D,連接BD.
(1)若∠A=40°,求∠DBC的度數(shù).
(2)若△BCD的周長為16cm,△ABC的周長為26cm,求BC的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(本題滿分8分)如圖,在△ABC中,AB=AC,∠DAC是△ABC的一個外角.
實踐與操作:
根據(jù)要求尺規(guī)作圖,并在圖中標明相應(yīng)字母(保留作圖痕跡,不寫作法).

(1)作∠DAC的平分線AM;
(2)作線段AC的垂直平分線,與AM交于點F,與BC邊交于點E,連接AE、CF.
猜想并證明:
判斷四邊形AECF的形狀并加以證明.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com