
【題目】小聰和小明沿同一條路同時從學校出發到寧波天一閣查閱資料,學校與天一閣的路程是4千米,小聰騎自行車,小明步行,當小聰從原路回到學校時,小明剛好到達天一閣,圖中折線O﹣A﹣B﹣C和線段OD分別表示兩人離學校的路程s(千米)與所經過的時間t(分鐘)之間的函數關系,請根據圖象回答下列問題:
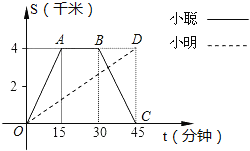
(1)小聰在天一閣查閱資料的時間為 分鐘,小聰返回學校的速度為 千米/分鐘;
(2)請你求出小明離開學校的路程s(千米)與所經過的時間t(分鐘)之間的函數關系;
(3)當小聰與小明迎面相遇時,他們離學校的路程是多少千米?
【答案】(1)15;![]() ;(2)s與t的函數關系式s=
;(2)s與t的函數關系式s=![]() t(0≤t≤45);(3)當小聰與小明迎面相遇時,他們離學校的路程是3千米.
t(0≤t≤45);(3)當小聰與小明迎面相遇時,他們離學校的路程是3千米.
【解析】
試題分析:(1)直接根據圖象上所給的數據的實際意義可求解;
(2)由圖象可知,s是t的正比例函數,設所求函數的解析式為s=kt(k≠0),把(45,4)代入解析式利用待定系數法即可求解;
(3)由圖象可知,小聰在30≤t≤45的時段內s是t的一次函數,設函數解析式為s=mt+n(m≠0)
把(30,4),(45,0)代入利用待定系數法先求得函數關系式,再根據求函數圖象的交點方法求得交點坐標即可.
解:(1)∵30﹣15=15,4÷15=![]()
∴小聰在天一閣查閱資料的時間和小聰返回學校的速度分別是15分鐘,![]() 千米/分鐘.
千米/分鐘.
(2)由圖象可知,s是t的正比例函數
設所求函數的解析式為s=kt(k≠0)
代入(45,4),得
4=45k
解得k=![]()
∴s與t的函數關系式s=![]() t(0≤t≤45).
t(0≤t≤45).
(3)由圖象可知,小聰在30≤t≤45的時段內s是t的一次函數,設函數解析式為s=mt+n(m≠0)
代入(30,4),(45,0),得
![]()
解得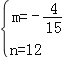
∴s=﹣![]() t+12(30≤t≤45)
t+12(30≤t≤45)
令﹣![]() t+12=
t+12=![]() t,解得t=
t,解得t=![]()
當t=![]() 時,S=
時,S=![]() ×
×![]() =3.
=3.
答:當小聰與小明迎面相遇時,他們離學校的路程是3千米.


科目:初中數學 來源: 題型:
【題目】如圖,已知AB∥CD,C在D的右側,BE平分∠ABC,DE平分∠ADC,BE、DE所在直線交于點E.∠ADC =70°.
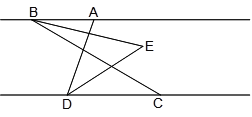
(1)求∠EDC的度數;
(2)若∠ABC =n°,求∠BED的度數(用含n的代數式表示);
(3)將線段BC沿DC方向平移, 使得點B在點A的右側,其他條件不變,畫出圖形并判斷∠BED的度數是否改變,若改變,求出它的度數(用含n的式子表示),不改變,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠C=90°,AC=3,BC=4,D是AB上一動點(不與A、B重合),DE⊥AC于點E,DF⊥BC于點F,點D由A向B移動時,矩形DECF的周長變化情況是( )
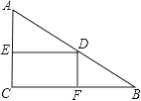
A. 逐漸減小 B. 逐漸增大 C. 先增大后減小 D. 先減小后增大
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com