
已知二次函數 .
.

1.當 時,函數值
時,函數值 隨
隨 的增大而減小,求
的增大而減小,求 的取值范圍;
的取值范圍;
2.以拋物線 的頂點
的頂點 為一個頂點作該拋物線的內接正
為一個頂點作該拋物線的內接正 (
( ,
, 兩點在拋物線上),請問:△
兩點在拋物線上),請問:△ 的面積是與
的面積是與 無關的定值嗎?若是,請求出這個定值;若不是,請說明理由;
無關的定值嗎?若是,請求出這個定值;若不是,請說明理由;
3.若拋物線 與
與 軸交點的橫坐標均為整數,求整數
軸交點的橫坐標均為整數,求整數 的值.
的值.
1.因為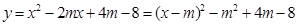
所以拋物線的對稱軸為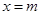 ,
………………
1分
,
………………
1分
因為要使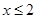 時,函數值y隨x的增大而減小,
時,函數值y隨x的增大而減小,
所以由圖像可知對稱軸應在直線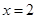 右側,從而m≥2.
右側,從而m≥2.
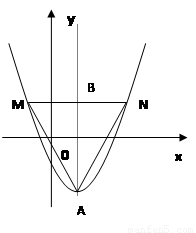
2.(方法一)根據拋物線和正三角形的對稱性,可知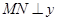 軸,設拋物線的對稱軸與
軸,設拋物線的對稱軸與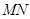 交于點
交于點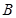 ,則
,則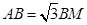 ,設
,設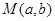 ,∴
,∴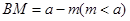 ,………………… 4分
,………………… 4分
又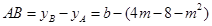
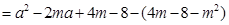
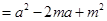
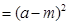 ,………………… 5分
,………………… 5分
∴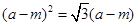 ,∴
,∴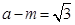 ,………………… 6分
,………………… 6分
∴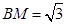 ,
,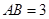 ,
,
∴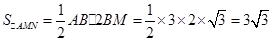 定值;…………………7分
定值;…………………7分
(方法二)由頂點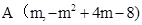 以及對稱性,設
以及對稱性,設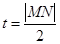 , ………………… 4分
, ………………… 4分
則M,N的坐標分別為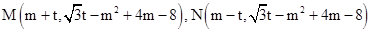 , 5分
, 5分
因為M,N兩點在拋物線上,
所以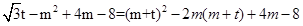 , ………………… 6分
, ………………… 6分
即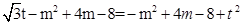 ,解得
,解得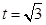 ,
,
所以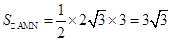 (與m無關);
(與m無關);
3.令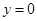 ,即
,即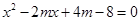 時,
時,
有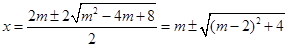 ,
………………… 9分
,
………………… 9分
由題意,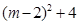 為完全平方數,令
為完全平方數,令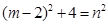 ,
,
即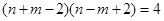 , ∵
, ∵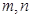 為整數,∴
為整數,∴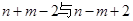 的奇偶性相同,
的奇偶性相同,
∴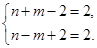 或
或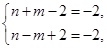 解得
解得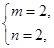 或
或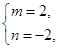
綜合得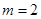 .
.
【解析】(1)根據拋物線的對稱軸求得
(2)根據拋物線和正三角形的對稱性,可知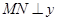 軸,設拋物線的對稱軸與
軸,設拋物線的對稱軸與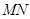 交于點
交于點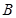 ,則
,則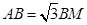 ,設
,設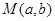 ,求得BM、AB的值,從而求得△
,求得BM、AB的值,從而求得△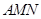 的面積
的面積
(3)令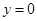 ,即
,即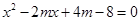 時,有x=
時,有x= 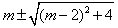 ,由題意,
,由題意,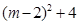 為完全平方數,令
為完全平方數,令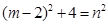 ,即
,即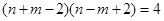 ,解方程求
,解方程求 值
值


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:初中數學 來源: 題型:
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•莒南縣二模)已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列5個結論:
(2013•莒南縣二模)已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列5個結論:查看答案和解析>>
科目:初中數學 來源: 題型:
 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:①ac>0;②a-b+c<0;
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:①ac>0;②a-b+c<0;查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com