
如圖,四邊形 是一張放在平面直角坐標系中的矩形紙片,點
是一張放在平面直角坐標系中的矩形紙片,點 在
在 軸上,點
軸上,點 在
在 軸上,將邊
軸上,將邊 折疊,使點
折疊,使點 落在邊
落在邊 的點
的點 處.已知折疊
處.已知折疊 ,且
,且 .
.
(1)判斷 與
與 是否相似?請說明理由;
是否相似?請說明理由;
(2)求直線 與
與 軸交點
軸交點 的坐標;
的坐標;
(3)是否存在過點 的直線
的直線 ,使直線
,使直線 、直線
、直線 與
與 軸所圍成的三角形和直線
軸所圍成的三角形和直線 、直線
、直線 與
與 軸所圍成的三角形相似?如果存在,請直接寫出其解析式并畫出相應的直線;如果不存在,請說明理由.
軸所圍成的三角形相似?如果存在,請直接寫出其解析式并畫出相應的直線;如果不存在,請說明理由.

解:(1) 與
與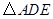 相似.
相似.
理由如下:

由折疊知,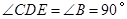 ,
,
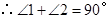 ,
,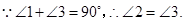
又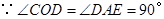 ,
,
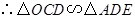 .
.
(2)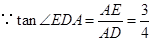 ,
, 設
設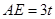 ,
,
則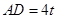 .
.
由勾股定理得 .
.
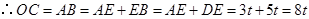 .
.
由(1)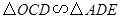 ,得
,得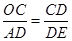 ,
,
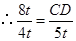 ,
,
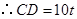 .
.
在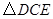 中,
中,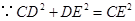 ,
,
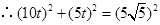 ,解得
,解得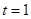 .
.
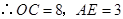 ,點
,點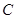 的坐標為
的坐標為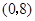 ,
,
點 的坐標為
的坐標為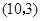 ,
,
設直線 的解析式為
的解析式為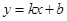 ,
,
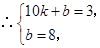 解得
解得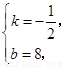
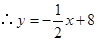 ,則點
,則點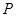 的坐標為
的坐標為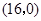 .
.
(3)滿足條件的直線 有2條:
有2條: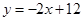 ,
,
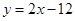 .
.
如圖2:準確畫出兩條直線.

【解析】(1)由折疊知,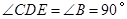 ,根據同角的余角相等可得
,根據同角的余角相等可得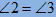 ,再有
,再有
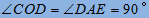 即可得到
即可得到 與
與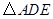 相似;
相似;
(2))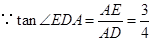 ,
, 設
設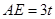 ,則
,則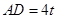 ,由勾股定理得
,由勾股定理得 ,
,
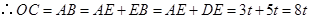 ,由(1)
,由(1)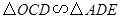 ,根據對應邊成比例可得
,根據對應邊成比例可得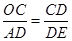 ,
,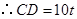 ,在
,在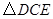 中根據勾股定義即可求出
中根據勾股定義即可求出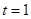 ,從而得到點
,從而得到點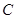 、點
、點 的坐標,再根據待定系數法即可得到直線
的坐標,再根據待定系數法即可得到直線 的解析式,從而得到點
的解析式,從而得到點 的坐標。
的坐標。
(3)存在,應該有兩條如圖:
①直線BF,根據折疊的性質可知CE必垂直平分BD,那么∠DGP=∠CGF=90°,而∠CFG=∠DPG(都是∠OCP的余角),由此可得出兩三角形相似,那么可根據B、D兩點的坐標求出此直線的解析式.
②直線DN,由于∠FCO=∠NDO,那么可根據∠OCE即∠BEC的正切值,求出∠NDO的正切值,然后用OD的長求出ON的值,即可求出N點的坐標,然后根據N、D兩點的坐標求出直線DN的解析式.


科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 4 |
| 1 |
| 4 |

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com