
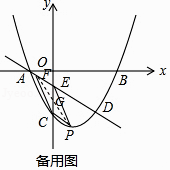
【題目】如圖,拋物線y= ![]() x2+bx+c經(jīng)過點(diǎn)B(3,0),C(0,﹣2),直線l:y=﹣
x2+bx+c經(jīng)過點(diǎn)B(3,0),C(0,﹣2),直線l:y=﹣ ![]() x﹣
x﹣ ![]() 交y軸于點(diǎn)E,且與拋物線交于A,D兩點(diǎn),P為拋物線上一動點(diǎn)(不與A,D重合).
交y軸于點(diǎn)E,且與拋物線交于A,D兩點(diǎn),P為拋物線上一動點(diǎn)(不與A,D重合).
(1)求拋物線的解析式;
(2)當(dāng)點(diǎn)P在直線l下方時,過點(diǎn)P作PM∥x軸交l于點(diǎn)M,PN∥y軸交l于點(diǎn)N,求PM+PN的最大值.
(3)設(shè)F為直線l上的點(diǎn),以E,C,P,F(xiàn)為頂點(diǎn)的四邊形能否構(gòu)成平行四邊形?若能,求出點(diǎn)F的坐標(biāo);若不能,請說明理由.
【答案】
(1)
解:把B(3,0),C(0,﹣2)代入y= ![]() x2+bx+c得,
x2+bx+c得, 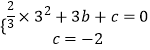 ,
,
∴ 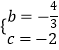
∴拋物線的解析式為:y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)
解:設(shè)P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),
m﹣2),
∵PM∥x軸,PN∥y軸,M,N在直線AD上,
∴N(m,﹣ ![]() m﹣
m﹣ ![]() ),M(﹣m2+2m+2,
),M(﹣m2+2m+2, ![]() m2﹣
m2﹣ ![]() m﹣2),
m﹣2),
∴PM+PN=﹣m2+2m+2﹣m﹣ ![]() m﹣
m﹣ ![]() ﹣
﹣ ![]() m2+
m2+ ![]() m+2=﹣
m+2=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() =﹣
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴當(dāng)m= ![]() 時,PM+PN的最大值是
時,PM+PN的最大值是 ![]()
(3)
解:能,
理由:∵y=﹣ ![]() x﹣
x﹣ ![]() 交y軸于點(diǎn)E,
交y軸于點(diǎn)E,
∴E(0,﹣ ![]() ),
),
∴CE= ![]() ,
,
設(shè)P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),
m﹣2),
∵以E,C,P,F(xiàn)為頂點(diǎn)的四邊形能否構(gòu)成平行四邊形,
①以CE為邊,∴CE∥PF,CE=PF,
∴F(m,﹣ ![]() m﹣
m﹣ ![]() ),
),
∴﹣ ![]() m﹣
m﹣ ![]() ﹣
﹣ ![]() m2+
m2+ ![]() m+2=
m+2= ![]() ,
,
∴m=1,m=0(舍去),
②以CE為對角線,連接PF交CE于G,
∴CG=GE,PG=FG,
∴G(0,﹣ ![]() ),
),
設(shè)P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),則F(﹣m,
m﹣2),則F(﹣m, ![]() m﹣
m﹣ ![]() ),
),
∴ ![]() ×(
×( ![]() m2﹣
m2﹣ ![]() m﹣2+
m﹣2+ ![]() m﹣
m﹣ ![]() )=﹣
)=﹣ ![]() ,
,
∵△<0,
∴此方程無實(shí)數(shù)根,
綜上所述,當(dāng)m=1時,以E,C,P,F(xiàn)為頂點(diǎn)的四邊形能否構(gòu)成平行四邊形.
【解析】(1.)把B(3,0),C(0,﹣2)代入y= ![]() x2+bx+c解方程組即可得到結(jié)論;(2.)設(shè)P(m,
x2+bx+c解方程組即可得到結(jié)論;(2.)設(shè)P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),得到N(m,﹣
m﹣2),得到N(m,﹣ ![]() m﹣
m﹣ ![]() ),M(﹣m2+2m+2,
),M(﹣m2+2m+2, ![]() m2﹣
m2﹣ ![]() m﹣2),根據(jù)二次函數(shù)的性質(zhì)即可得到結(jié)論;
m﹣2),根據(jù)二次函數(shù)的性質(zhì)即可得到結(jié)論;
(3.)求得E(0,﹣ ![]() ),得到CE=
),得到CE= ![]() ,設(shè)P(m,
,設(shè)P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),①以CE為邊,根據(jù)CE=PF,列方程得到m=1,m=0(舍去),②以CE為對角線,連接PF交CE于G,CG=GE,PG=FG,得到G(0,﹣
m﹣2),①以CE為邊,根據(jù)CE=PF,列方程得到m=1,m=0(舍去),②以CE為對角線,連接PF交CE于G,CG=GE,PG=FG,得到G(0,﹣ ![]() ),設(shè)P(m,
),設(shè)P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),則F(﹣m,
m﹣2),則F(﹣m, ![]() m﹣
m﹣ ![]() ),列方程得到此方程無實(shí)數(shù)根,于是得到結(jié)論.
),列方程得到此方程無實(shí)數(shù)根,于是得到結(jié)論.
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解求根公式的相關(guān)知識,掌握根的判別式△=b2-4ac,這里可以分為3種情況:1、當(dāng)△>0時,一元二次方程有2個不相等的實(shí)數(shù)根2、當(dāng)△=0時,一元二次方程有2個相同的實(shí)數(shù)根3、當(dāng)△<0時,一元二次方程沒有實(shí)數(shù)根,以及對二次函數(shù)的性質(zhì)的理解,了解增減性:當(dāng)a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當(dāng)a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,點(diǎn)O是邊AC上一個動點(diǎn),過點(diǎn)O作直線EF∥BC分別交∠ACB、外角∠ACD的平分線于點(diǎn)E、F.
(1)若CE=8,CF=6,求OC的長;
(2)連接AE、AF.問:當(dāng)點(diǎn)O在邊AC上運(yùn)動到什么位置時,四邊形AECF是矩形?并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列運(yùn)算正確的是( )
A.(x﹣y)2=x2﹣y2
B.| ![]() ﹣2|=2﹣
﹣2|=2﹣ ![]()
C.![]() ﹣
﹣ ![]() =
= ![]()
D.﹣(﹣a+1)=a+1
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為確保廣大居民家庭基本用水需求的同時鼓勵家庭節(jié)約用水,對居民家庭每戶每月用水量采用分檔遞增收費(fèi)的方式,每戶每月用水量不超過基本用水量的部分享受基本價格,超出基本用水量的部分實(shí)行超價收費(fèi).為對基本用水量進(jìn)行決策,隨機(jī)抽查2000戶居民家庭每戶每月用水量的數(shù)據(jù),整理繪制出下面的統(tǒng)計(jì)表:
用戶每月用水量(m3) | 32及其以下 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43及其以上 |
戶數(shù)(戶) | 200 | 160 | 180 | 220 | 240 | 210 | 190 | 100 | 170 | 120 | 100 | 110 |
(1)為確保70%的居民家庭每戶每月的基本用水量需求,那么每戶每月的基本用水量最低應(yīng)確定為多少立方米?
(2)若將(1)中確定的基本用水量及其以內(nèi)的部分按每立方米1.8元交費(fèi),超過基本用水量的部分按每立方米2.5元交費(fèi).設(shè)x表示每戶每月用水量(單位:m3),y表示每戶每月應(yīng)交水費(fèi)(單位:元),求y與x的函數(shù)關(guān)系式;
(3)某戶家庭每月交水費(fèi)是80.9元,請按以上收費(fèi)方式計(jì)算該家庭當(dāng)月用水量是多少立方米?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】求證:對角線互相垂直的平行四邊形是菱形.
小紅同學(xué)根據(jù)題意畫出了圖形,并寫出了已知和求證的一部分,請你補(bǔ)全已知和求證,并寫出證明過程.
①已知:如圖,在ABCD中,對角線AC,BD交于點(diǎn)O,________.
②求證:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某游樂場部分平面圖如圖所示,C、E、A在同一直線上,D、E、B在同一直線上,測得A處與E處的距離為80 米,C處與D處的距離為34米,∠C=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7) 
(1)求旋轉(zhuǎn)木馬E處到出口B處的距離;
(2)求海洋球D處到出口B處的距離(結(jié)果保留整數(shù)).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了備戰(zhàn)初三物理、化學(xué)實(shí)驗(yàn)操作考試,某校對初三學(xué)生進(jìn)行了模擬訓(xùn)練,物理、化學(xué)各有4各不同的操作實(shí)驗(yàn)題目,物理用番號①、②、③、④代表,化學(xué)用字母a、b、c、d表示,測試時每名學(xué)生每科只操作一個實(shí)驗(yàn),實(shí)驗(yàn)的題目由學(xué)生抽簽確定,第一次抽簽確定物理實(shí)驗(yàn)題目,第二次抽簽確定化學(xué)實(shí)驗(yàn)題目.
(1)請用樹形圖法或列表法,表示某個同學(xué)抽簽的各種可能情況.
(2)小張同學(xué)對物理的①、②和化學(xué)的b、c號實(shí)驗(yàn)準(zhǔn)備得較好,他同時抽到兩科都準(zhǔn)備的較好的實(shí)驗(yàn)題目的概率是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】
(1)計(jì)算:(﹣1)2011+ ![]() ﹣2sin60°+|﹣1|.
﹣2sin60°+|﹣1|.
(2)解不等式組  ,并把它的解集在數(shù)軸上表示出來.
,并把它的解集在數(shù)軸上表示出來.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸的交點(diǎn)為A、D(A在D的右側(cè)),與y軸的交點(diǎn)為C,且A(4,0),C(0,﹣3),對稱軸是直線x=1.
(1)求二次函數(shù)的解析式;
(2)若M是第四象限拋物線上一動點(diǎn),且橫坐標(biāo)為m,設(shè)四邊形OCMA的面積為s.請寫出s與m之間的函數(shù)關(guān)系式,并求出當(dāng)m為何值時,四邊形OCMA的面積最大;
(3)設(shè)點(diǎn)B是x軸上的點(diǎn),P是拋物線上的點(diǎn),是否存在點(diǎn)P,使得以A,B、C,P四點(diǎn)為頂點(diǎn)的四邊形為平行四邊形?若存在,直接寫出點(diǎn)P的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com