
【題目】(本小題滿分13分)設關于![]() 的一元二次方程
的一元二次方程![]()
![]()
![]()
![]()
![]()
![]()
![]() (
(![]() )有兩根
)有兩根![]() 和
和![]() ,且滿足
,且滿足![]() .
.
(1)試用![]() 表示
表示![]() ;
;
(2)求證:數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(3)當![]() 時,求數(shù)列
時,求數(shù)列![]() 的通項公式,并求數(shù)列
的通項公式,并求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() ;(2)詳見解析;(3)
;(2)詳見解析;(3)![]()
【解析】
試題分析:(1)由韋達定理可得![]() ,
,![]() ,代入已知
,代入已知![]() 和
和![]() 關系式可得
關系式可得![]() 與
與![]() 的關系式.(2)由(1)中所得的
的關系式.(2)由(1)中所得的![]() 與
與![]() 的關系式,根據(jù)等比數(shù)列的定義證
的關系式,根據(jù)等比數(shù)列的定義證 為常數(shù).(3)根據(jù)等比數(shù)列的通項公式可先求得
為常數(shù).(3)根據(jù)等比數(shù)列的通項公式可先求得![]() ,從而可得
,從而可得![]() .根據(jù)分組求和及錯位相減法可求得數(shù)列
.根據(jù)分組求和及錯位相減法可求得數(shù)列![]() 的前
的前![]() 項和.
項和.
試題解析:解:(1)根據(jù)韋達定理,得![]() ,
,![]() ,
,
由![]()
得 ![]() ,故
,故![]()
(2)證明:![]() ,
,
若![]() ,則
,則![]() ,從而
,從而![]() ,
,
這時一元二次方程![]()
![]()
![]()
![]()
![]()
![]()
![]() 無實數(shù)根,故
無實數(shù)根,故![]() ,
,
所以 ,數(shù)列
,數(shù)列![]() 是公比為
是公比為![]() 的等比數(shù)列.
的等比數(shù)列.
(3)設![]() ,則數(shù)列
,則數(shù)列![]() 是公比
是公比![]() 的等比數(shù)列,
的等比數(shù)列,
又![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() .
.
![]()
則由錯位相減法可得![]()
![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)f(x)= ![]() ﹣2x+ln(x+1)(m∈R).
﹣2x+ln(x+1)(m∈R).
(Ⅰ)判斷x=1能否為函數(shù)f(x)的極值點,并說明理由;
(Ⅱ)若存在m∈[﹣4,﹣1),使得定義在[1,t]上的函數(shù)g(x)=f(x)﹣ln(x+1)+x3在x=1處取得最大值,求實數(shù)t的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 是首項為正數(shù)的等差數(shù)列,數(shù)列
是首項為正數(shù)的等差數(shù)列,數(shù)列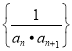 的前
的前![]() 項和為
項和為![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列{an}的前n項和為Sn . 若對任意正整數(shù)n,總存在正整數(shù)m,使得Sn=am , 則稱{an}是“H數(shù)列”.
(1)若數(shù)列{an}的前n項和Sn=2n(n∈N*),證明:{an}是“H數(shù)列”;
(2)設{an}是等差數(shù)列,其首項a1=1,公差d<0.若{an}是“H數(shù)列”,求d的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點P是圓F1:(x﹣1)2+y2=8上任意一點,點F2與點F1關于原點對稱,線段PF2的垂直平分線分別與PF1,PF2交于M,N兩點.
(1)求點M的軌跡C的方程;
(2)過點G(0, ![]() )的動直線l與點的軌跡C交于A,B兩點,在y軸上是否存在定點Q,使以AB為直徑的圓恒過這個點?若存在,求出點Q的坐標;若不存在,請說明理由.
)的動直線l與點的軌跡C交于A,B兩點,在y軸上是否存在定點Q,使以AB為直徑的圓恒過這個點?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,a,b,c分別為內角A,B,C的對邊,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,PA⊥平面ABCD,底面ABCD為直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2 ![]() ,PA=4且E為PB的中點.
,PA=4且E為PB的中點. 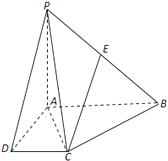
(1)求證:CE∥平面PAD;
(2)求直線CE與平面PAC所成角的正弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com