
【題目】已知數列![]() 滿足
滿足![]() .
.
(1)證明:數列![]() 為等差數列;
為等差數列;
(2)設數列![]() 的前n項和為
的前n項和為![]() ,若
,若![]() ,且對任意的正整數n,都有
,且對任意的正整數n,都有![]() ,求整數
,求整數![]() 的值;
的值;
(3)設數列![]() 滿足
滿足![]() ,若
,若![]() ,且存在正整數s,t,使得
,且存在正整數s,t,使得![]() 是整數,求
是整數,求![]() 的最小值.
的最小值.
【答案】(1)證明見解析;(2)2;(3)![]()
【解析】
(1)令![]() 中的
中的![]() 為
為![]() ,又得一式,將兩式做差變形,利用等差中項進行證明;
,又得一式,將兩式做差變形,利用等差中項進行證明;
(2)利用放縮法和裂項相消法在數列求和中的應用進行證明.
(3)利用假設法的應用和存在性問題的應用求出最小值.
解:(1)因為![]() ①
①
所以![]() 時,
時,![]() ②
②
①-②得![]() ,
,
所以![]()
即![]()
所以數列![]() 為等差數列;
為等差數列;
(2)因為![]() ,所以
,所以![]() 的公差為1,
的公差為1,
因為對任意的正整數![]() ,都有
,都有![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 或2,
或2,
當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,這與題意矛盾,所以
,這與題意矛盾,所以![]() ,
,
當![]() 時,
時,![]() ,
,
![]() ,
,
![]() ,
,![]() 恒成立,
恒成立,
因為![]() ,
,
![]()
![]() ,
,
綜上,![]() 的值為2.
的值為2.
(3)因為![]() ,所以
,所以![]() 的公差為
的公差為![]() ,
,
所以![]() ,
,
所以![]() ,
,
由題意,設存在正整數s,t,使得![]() ,
,![]() ,
,
則![]() ,即
,即![]() ,
,
因為![]() ,
,
所以![]() 是偶數,
是偶數,
所以![]() ,
,
所以![]() ,
,
當![]() 時,
時,![]() ,
,
所以存在![]() ,
,
綜上,![]() 的最小值為
的最小值為![]() .
.


科目:高中數學 來源: 題型:
【題目】關于數列![]() ,給出下列命題:①數列
,給出下列命題:①數列![]() 滿足
滿足![]() ,則數列
,則數列![]() 為公比為2的等比數列;②“
為公比為2的等比數列;②“![]() ,
,![]() 的等比中項為
的等比中項為![]() ”是“
”是“![]() ”的充分不必要條件:③數列
”的充分不必要條件:③數列![]() 是公比為
是公比為![]() 的等比數列,則其前
的等比數列,則其前![]() 項和
項和![]() ;④等比數列
;④等比數列![]() 的前
的前![]() 項和為
項和為![]() ,則
,則![]() ,
,![]() ,
,![]() 成等比數列,其中假命題的序號是( )
成等比數列,其中假命題的序號是( )
A.②B.②④C.①②④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了選拔學生參加“XX市中學生知識競賽”,先在本校進行選拔測試,若該校有100名學生參加選拔測試,并根據選拔測試成績作出如圖所示的頻率分布直方圖.
(1)根據頻率分布直方圖,估算這100名學生參加選拔測試的平均成績;
(2)該校推薦選拔測試成績在110以上的學生代表學校參加市知識競賽,為了了解情況,在該校推薦參加市知識競賽的學生中隨機抽取2人,求選取的兩人的選拔成績在頻率分布直方圖中處于不同組的概率.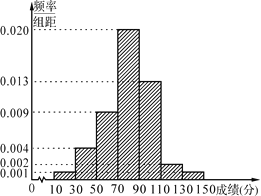
查看答案和解析>>
科目:高中數學 來源: 題型:
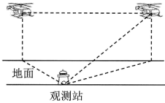
【題目】2019年10月1日,在慶祝新中國成立70周年閱兵中,由我國自主研制的軍用飛機和軍用無人機等參閱航空裝備分秒不差飛越天安門,壯軍威,振民心,令世人矚目.飛行員高超的飛行技術離不開艱苦的訓練和科學的數據分析.一次飛行訓練中,地面觀測站觀測到一架參閱直升飛機以![]() 千米/小時的速度在同一高度向正東飛行,如圖,第一次觀測到該飛機在北偏西
千米/小時的速度在同一高度向正東飛行,如圖,第一次觀測到該飛機在北偏西![]() 的方向上,1分鐘后第二次觀測到該飛機在北偏東
的方向上,1分鐘后第二次觀測到該飛機在北偏東![]() 的方向上,仰角為
的方向上,仰角為![]() ,則直升機飛行的高度為________千米.(結果保留根號)
,則直升機飛行的高度為________千米.(結果保留根號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有人玩擲均勻硬幣走跳棋的游戲,棋盤上標有第0站(出發地),在第1站,第2站,……,第100站. 一枚棋子開始在出發地,棋手每擲一次硬幣,這枚棋子向前跳動一次,若擲出正向,棋子向前跳一站,若擲出反面,棋子向前跳兩站,直到棋子跳到第99站(失敗收容地)或跳到第100站(勝利大本營),該游戲結束. 設棋子跳到第![]() 站的概率為
站的概率為![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)寫出![]() 與
與![]() 、
、![]() 的遞推關系
的遞推關系![]() );
);
(3)求玩該游戲獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() ,
,![]() ,設
,設![]() ,
,![]() ,其中
,其中![]() 為坐標原點.
為坐標原點.
(1)設點![]() 在
在![]() 軸上方,到線段
軸上方,到線段![]() 所在直線的距離為
所在直線的距離為![]() ,且
,且![]() ,求
,求![]() 和線段
和線段![]() 的大小;
的大小;
(2)設點![]() 為線段
為線段![]() 的中點,若
的中點,若![]() ,且點
,且點![]() 在第二象限內,求
在第二象限內,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的左頂點為
的左頂點為![]() ,過
,過![]() 的直線交橢圓
的直線交橢圓![]() 于另一點
于另一點![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() .
.
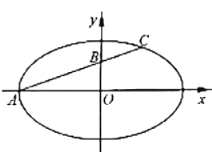
(1)求橢圓![]() 的離心率;
的離心率;
(2)若橢圓![]() 的焦距為
的焦距為![]() ,
,![]() 為橢圓
為橢圓![]() 上一點,線段
上一點,線段![]() 的垂直平分線
的垂直平分線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() (
(![]() 不與
不與![]() 軸重合),求直線
軸重合),求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com