
(1)解不等式: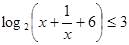 ;
;
(2)已知集合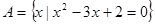 ,
,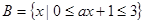 .若
.若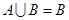 ,求實(shí)數(shù)
,求實(shí)數(shù)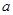 的取值組成的集合.
的取值組成的集合.
(1)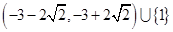 ;(2)
;(2)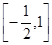 .
.
解析試題分析:(1)本題是一個(gè)對(duì)數(shù)不等式問題的求解問題,解不等式時(shí),先由對(duì)數(shù)函數(shù)的單調(diào)性得到真數(shù)的取值范圍,不要忘記了真數(shù)為正的要求,此時(shí)就可化為一般的分式不等式解之即可,分式不等式要去分母時(shí),要注意符號(hào)的討論;(2)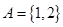 ,由
,由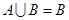 知
知 ,要具體化集合
,要具體化集合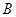 的過程中,要解一個(gè)含有參數(shù)的不等式,要對(duì)參數(shù)進(jìn)行分類討論,然后對(duì)各種情況下的結(jié)果利用
的過程中,要解一個(gè)含有參數(shù)的不等式,要對(duì)參數(shù)進(jìn)行分類討論,然后對(duì)各種情況下的結(jié)果利用 解決問題,較為簡(jiǎn)單的做法是,集合
解決問題,較為簡(jiǎn)單的做法是,集合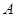 中的元素都在集合
中的元素都在集合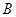 ,都滿足不等式,代入即可解決問題.
,都滿足不等式,代入即可解決問題.
試題解析:(1)由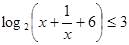 得,
得,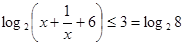
∴ .
.
由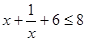 解得
解得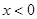 或
或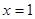
由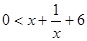 解得
解得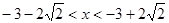 或
或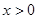
從而得原不等式的解集為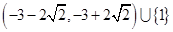 .
.
(2)法一:∵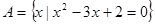
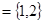 ,
,
又∵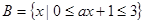
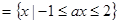 ,
,
∵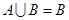 ,∴
,∴
①當(dāng)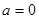 時(shí),
時(shí),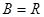 ,滿足題意.
,滿足題意.
②當(dāng) 時(shí),
時(shí),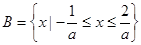 ,∵
,∵ ∴
∴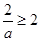 ,解得
,解得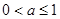 .
.
③當(dāng)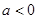 時(shí),
時(shí),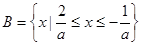 ,∵
,∵ ∴
∴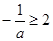 ,解得
,解得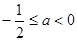 .
.
綜上,實(shí)數(shù)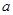 的取值組成的集合為
的取值組成的集合為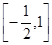 .
.
法二:∵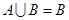 ,∴
,∴
又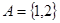 ,∴
,∴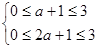 ∴
∴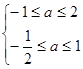 ,∴
,∴ .
.
∴實(shí)數(shù)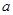 的取值組成的集合為
的取值組成的集合為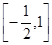 .
.
考點(diǎn):對(duì)數(shù)函數(shù)的性質(zhì)、解不等式、集合的包含關(guān)系.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
某連鎖分店銷售某種商品,每件商品的成本為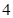 元,并且每件商品需向總店交
元,并且每件商品需向總店交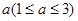 元的管理費(fèi),預(yù)計(jì)當(dāng)每件商品的售價(jià)為
元的管理費(fèi),預(yù)計(jì)當(dāng)每件商品的售價(jià)為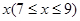 元時(shí),一年的銷售量為
元時(shí),一年的銷售量為 萬件.
萬件.
(Ⅰ)求該連鎖分店一年的利潤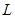 (萬元)與每件商品的售價(jià)
(萬元)與每件商品的售價(jià)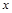 的函數(shù)關(guān)系式
的函數(shù)關(guān)系式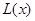 ;
;
(Ⅱ)當(dāng)每件商品的售價(jià)為多少元時(shí),該連鎖分店一年的利潤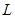 最大,并求出
最大,并求出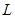 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)f(x)=x2x+13,實(shí)數(shù)a滿足|xa|<1,求證:|f(x)f(a)|<2(|a|+1).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)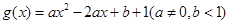 在區(qū)間
在區(qū)間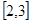 上有最大值4,最小值1,
上有最大值4,最小值1,
(Ⅰ)求 的值。
的值。
(Ⅱ)設(shè)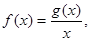 不等式
不等式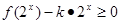 在區(qū)間
在區(qū)間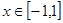 上恒成立,求實(shí)數(shù)k的取值范圍?
上恒成立,求實(shí)數(shù)k的取值范圍?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
一企業(yè)生產(chǎn)的某產(chǎn)品在不做電視廣告的前提下,每天銷售量為b噸.經(jīng)市場(chǎng)調(diào)查后得到如下規(guī)律:若對(duì)產(chǎn)品進(jìn)行電視廣告的宣傳,每天的銷售量S(噸)與電視廣告每天的播放量n(次)的關(guān)系可用如圖所示的程序框圖來體現(xiàn).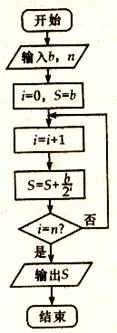
(1)試寫出該產(chǎn)品每天的銷售量S(噸)關(guān)于電視廣告每天的播放量n(次)的函數(shù)關(guān)系式;
(2)要使該產(chǎn)品每天的銷售量比不做電視廣告時(shí)的銷售量至少增加90%,則每天電視廣告的播放量至少需多少次?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
近年來,網(wǎng)上購物已經(jīng)成為人們消費(fèi)的一種趨勢(shì)。假設(shè)某淘寶店的一種裝飾品每月的銷售量y(單位:千件)與銷售價(jià)格x(單位:元/件)滿足關(guān)系式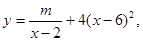 其中2<x<6,m為常數(shù),已知銷售價(jià)格為4元/件時(shí),每月可售出21千件。(1)求m的值; (2)假設(shè)該淘寶店員工工資、辦公等每月所有開銷折合為每件2元(只考慮銷售出的件數(shù)),試確定銷售價(jià)格x的值,使該店每月銷售飾品所獲得的利潤最大.(結(jié)果保留一位小數(shù))
其中2<x<6,m為常數(shù),已知銷售價(jià)格為4元/件時(shí),每月可售出21千件。(1)求m的值; (2)假設(shè)該淘寶店員工工資、辦公等每月所有開銷折合為每件2元(只考慮銷售出的件數(shù)),試確定銷售價(jià)格x的值,使該店每月銷售飾品所獲得的利潤最大.(結(jié)果保留一位小數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 函數(shù)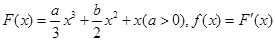 ,若
,若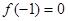 且對(duì)任意實(shí)數(shù)
且對(duì)任意實(shí)數(shù)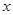 均有
均有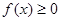 成立.
成立.
(1)求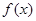 表達(dá)式;
表達(dá)式;
(2)當(dāng)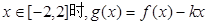 是單調(diào)函數(shù),求實(shí)數(shù)
是單調(diào)函數(shù),求實(shí)數(shù)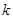 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
定義在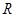 上的函數(shù)
上的函數(shù)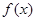 對(duì)任意
對(duì)任意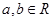 都有
都有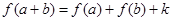 (
(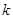 為常數(shù)).
為常數(shù)).
(1)判斷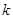 為何值時(shí)
為何值時(shí)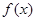 為奇函數(shù),并證明;
為奇函數(shù),并證明;
(2)設(shè)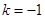 ,
,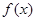 是
是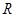 上的增函數(shù),且
上的增函數(shù),且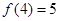 ,若不等式
,若不等式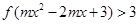 對(duì)任意
對(duì)任意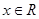 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)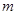 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com