
【題目】在平面直角坐標(biāo)系![]() 中,已知橢圓
中,已知橢圓![]() :
: ![]() 的離心率
的離心率![]() ,且橢圓
,且橢圓![]() 上一點(diǎn)
上一點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的距離最大值為4,過(guò)點(diǎn)
的距離最大值為4,過(guò)點(diǎn)![]() 的直線交橢圓
的直線交橢圓![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 為橢圓上一點(diǎn),且滿足
為橢圓上一點(diǎn),且滿足![]() (
(![]() 為坐標(biāo)原點(diǎn)),當(dāng)
為坐標(biāo)原點(diǎn)),當(dāng)![]() 時(shí),求實(shí)數(shù)
時(shí),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】試題分析:(1)由離心率![]() 及
及![]() 可得關(guān)于
可得關(guān)于![]() 的方程,由此可簡(jiǎn)化橢圓方程,設(shè)
的方程,由此可簡(jiǎn)化橢圓方程,設(shè)![]() ,則
,則![]() 可表示為
可表示為![]() 的函數(shù),據(jù)此可求得其最大值,解得
的函數(shù),據(jù)此可求得其最大值,解得![]() ,即可求出橢圓
,即可求出橢圓![]() 的方程;(2)設(shè)
的方程;(2)設(shè)![]() ,
, ![]() ,
, ![]() ,
, ![]() 的方程為
的方程為![]() ,與橢圓聯(lián)立方程消掉
,與橢圓聯(lián)立方程消掉![]() 得關(guān)于
得關(guān)于![]() 的一元二次方程,由
的一元二次方程,由![]() 得
得![]() ,由韋達(dá)定理及
,由韋達(dá)定理及![]() 可用
可用![]() 表示出點(diǎn)
表示出點(diǎn)![]() 的坐標(biāo),代入橢圓方程得
的坐標(biāo),代入橢圓方程得![]() ,再由弦長(zhǎng)公式及
,再由弦長(zhǎng)公式及![]() 可得
可得![]() ,即可求出實(shí)數(shù)
,即可求出實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
試題解析:(1)∵![]()
∴![]() ,則橢圓方程為
,則橢圓方程為![]() ,即
,即![]()
設(shè)![]() ,則
,則![]()
當(dāng)![]() 時(shí),
時(shí), ![]() 有最大值為
有最大值為![]() ,
,
解得![]()
∴![]() ,橢圓方程是
,橢圓方程是![]()
(2)設(shè)![]() ,
, ![]() ,
, ![]() ,
, ![]() 的方程為
的方程為![]() ,
,
由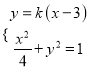 ,整理得
,整理得![]()
由![]() ,得
,得![]()
![]() ,
, ![]() ,
,
∴![]() ,
,
則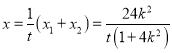 ,
, 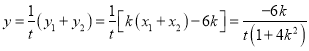
由點(diǎn)![]() 在橢圓上,得
在橢圓上,得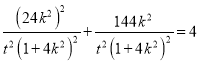
化簡(jiǎn)得![]() ①
①
又由![]() ,即
,即
![]() ,將
,將![]() ,
, ![]() 代入得
代入得
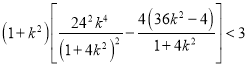 ,
,
化簡(jiǎn),得![]() ,
,
則![]()
∴![]() ②
②
由①,得![]() ,
,
聯(lián)立②,解得![]()
∴![]() 或
或![]()


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,三棱臺(tái)![]() 中, 側(cè)面
中, 側(cè)面![]() 與側(cè)面
與側(cè)面![]() 是全等的梯形,若
是全等的梯形,若![]() ,且
,且![]() .
.

(Ⅰ)若![]() ,
, ![]() ,證明:
,證明: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若二面角![]() 為
為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著資本市場(chǎng)的強(qiáng)勢(shì)進(jìn)入,互聯(lián)網(wǎng)共享單車“忽如一夜春風(fēng)來(lái)”,遍布了一二線城市的大街小巷.為了解共享單車在![]() 市的使用情況,某調(diào)查機(jī)構(gòu)借助網(wǎng)絡(luò)進(jìn)行了問(wèn)卷調(diào)查,并從參與調(diào)查的網(wǎng)友中抽取了200人進(jìn)行抽樣分析,得到表格:(單位:人)
市的使用情況,某調(diào)查機(jī)構(gòu)借助網(wǎng)絡(luò)進(jìn)行了問(wèn)卷調(diào)查,并從參與調(diào)查的網(wǎng)友中抽取了200人進(jìn)行抽樣分析,得到表格:(單位:人)
經(jīng)常使用 | 偶爾或不用 | 合計(jì) | |
30歲及以下 | 70 | 30 | 100 |
30歲以上 | 60 | 40 | 100 |
合計(jì) | 130 | 70 | 200 |
(1)根據(jù)以上數(shù)據(jù),能否在犯錯(cuò)誤的概率不超過(guò)0.15的前提下認(rèn)為![]() 市使用共享單車情況與年齡有關(guān)?
市使用共享單車情況與年齡有關(guān)?
(2)現(xiàn)從所抽取的30歲以上的網(wǎng)友中利用分層抽樣的方法再抽取5人.從這5人中,再隨機(jī)選出2人贈(zèng)送一件禮品,求選出的2人中至少有1人經(jīng)常使用共享單車的概率.
參考公式: 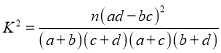 ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() ,
,![]() .
.
(I)若![]() ,求函數(shù)
,求函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(II)若函數(shù)![]() 在
在![]() 上是增函數(shù),求實(shí)數(shù)
上是增函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(III)令![]() ,
,![]() (
(![]() 是自然對(duì)數(shù)的底數(shù)),求當(dāng)實(shí)數(shù)
是自然對(duì)數(shù)的底數(shù)),求當(dāng)實(shí)數(shù)![]() 等于多少時(shí),可以使函數(shù)
等于多少時(shí),可以使函數(shù)![]() 取得最小值為3.
取得最小值為3.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩人進(jìn)行射擊比賽,各射擊![]() 局,每局射擊
局,每局射擊![]() 次,射擊命中目標(biāo)得
次,射擊命中目標(biāo)得![]() 分,未命中目標(biāo)得
分,未命中目標(biāo)得![]() 分,兩人
分,兩人![]() 局的得分情況如下:
局的得分情況如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(Ⅰ)若從甲的![]() 局比賽中,隨機(jī)選取
局比賽中,隨機(jī)選取![]() 局,求這
局,求這![]() 局的得分恰好相等的概率.
局的得分恰好相等的概率.
(Ⅱ)如果![]() ,從甲、乙兩人的
,從甲、乙兩人的![]() 局比賽中隨機(jī)各選取
局比賽中隨機(jī)各選取![]() 局,記這
局,記這![]() 局的得分和為
局的得分和為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
(Ⅲ)在![]() 局比賽中,若甲、乙兩人的平均得分相同,且乙的發(fā)揮更穩(wěn)定,寫出
局比賽中,若甲、乙兩人的平均得分相同,且乙的發(fā)揮更穩(wěn)定,寫出![]() 的所有可能取值.(結(jié)論不要求證明)
的所有可能取值.(結(jié)論不要求證明)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
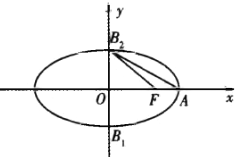
【題目】如圖,已知![]() 為橢圓
為橢圓![]() :
: ![]() 的右焦點(diǎn),
的右焦點(diǎn), ![]() ,
, ![]() ,
, ![]() 為橢圓的下、上、右三個(gè)頂點(diǎn),
為橢圓的下、上、右三個(gè)頂點(diǎn), ![]() 與
與![]() 的面積之比為
的面積之比為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)試探究在橢圓![]() 上是否存在不同于點(diǎn)
上是否存在不同于點(diǎn)![]() ,
, ![]() 的一點(diǎn)
的一點(diǎn)![]() 滿足下列條件:點(diǎn)
滿足下列條件:點(diǎn)![]() 在
在![]() 軸上的投影為
軸上的投影為![]() ,
, ![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,直線
,直線![]() 交直線
交直線![]() 于點(diǎn)
于點(diǎn)![]() ,
, ![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,且
,且![]() 的面積為
的面積為![]() .若不存在,請(qǐng)說(shuō)明理由;若存在,求出點(diǎn)
.若不存在,請(qǐng)說(shuō)明理由;若存在,求出點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
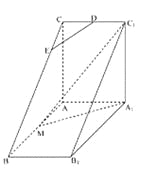
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() 是等腰三角形,
是等腰三角形,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 上一點(diǎn).
上一點(diǎn).
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 將三棱柱
將三棱柱![]() 分成兩個(gè)部分,求較小部分與較大部分的體積之比.
分成兩個(gè)部分,求較小部分與較大部分的體積之比.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為實(shí)數(shù)).
為實(shí)數(shù)).
(Ⅰ)若![]() ,求函數(shù)
,求函數(shù)![]() 在
在![]() 處的切線方程.
處的切線方程.
(Ⅱ)求函數(shù)![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
(Ⅲ)若存在![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com