
先后2次拋擲一枚骰子,將得到的點數分別記為a,b.
(1)求直線ax+by+5=0與圓x2+y2=1相切的概率;
(2)將a,b,5的值分別作為三條線段的長,求這三條線段能圍成等腰三角形的概率.
(1)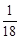 ;(2)
;(2)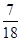
解析試題分析:(1)先后2次拋擲一枚骰子,將得到的點數分別記為a,b,事件總數為6×6=36.
∵直線ax+by+c=0與圓x2+y2=1相切的充要條件是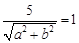 即:a2+b2=25,……2分
即:a2+b2=25,……2分
由于a,b∈{1,2,3,4,5,6}
∴滿足條件的情況只有a=3,b=4,c=5;或a=4,b=3,c=5兩種情況. ……4分
∴直線ax+by+c=0與圓x2+y2=1相切的概率是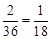 ……6分
……6分
(2)先后2次拋擲一枚骰子,將得到的點數分別記為a,b,事件總數為6×6=36.
∵三角形的一邊長為5 ∴當a=1時,b=5,(1,5,5) 1種
當a=2時,b=5,(2,5,5) 1種
當a=3時,b=3,5,(3,3,5),(3,5,5) 2種
當a=4時,b=4,5,(4,4,5),(4,5,5) 2種
當a=5時,b=1,2,3,4,5,6, (5,1,5),(5,2,5),(5,3,5),
(5,4,5),(5,5,5),(5,6,5) 6種
當a=6時,b=5,6,(6,5,5),(6,6,5) 2種
故滿足條件的不同情況共有14種 ……12分
答:三條線段能圍成不同的等腰三角形的概率為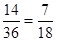 . ……14分
. ……14分
考點:本題考查了古典概型的應用,考查了學生分析問題解決問題的能力。
點評:對于古典概型的概率的計算,首先要分清基本事件總數及事件 包含的基本事件數,分清的方法常用列表法、畫圖法、列舉法、列式計算等方法。
包含的基本事件數,分清的方法常用列表法、畫圖法、列舉法、列式計算等方法。


科目:高中數學 來源: 題型:解答題
已知甲盒內有大小相同的1個紅球和3個黑球, 乙盒內有大小相同的2個紅球和4個黑球,現從甲、乙兩個盒內各任取2個球.
(Ⅰ)求取出的4個球均為黑球的概率;
(Ⅱ)求取出的4個球中恰有1個紅球的概率;
(Ⅲ)設 為取出的4個球中紅球的個數,求
為取出的4個球中紅球的個數,求 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩個盒子里各放有標號為1,2,3,4的四個大小形狀完全相同的小球,從甲盒中任取一小球,記下號碼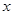 后放入乙盒,再從乙盒中任取一小球,記下號碼
后放入乙盒,再從乙盒中任取一小球,記下號碼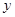 .
.
(Ⅰ)求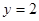 的概率;
的概率;
(Ⅱ)設隨機變量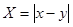 ,求隨機變量
,求隨機變量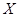 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)盒中有大小相同的編號為1,2,3,4,5,6的六只小球,規定:從盒中一次摸出'2只球,如果這2只球的編號均能被3整除,則獲一等獎,獎金10元,如果這2只球的編號均為偶數,則獲二等獎,獎金2元,其他情況均不獲獎.
(1)若某人參加摸球游戲一次獲獎金x元,求x的分布列及期望;
(2)若某人摸一次且獲獎,求他獲得一等獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
在一次數學考試中共有8道選擇題,每道選擇題都有4個選項,其中有且只有一個選項是正確的.某考生有5道題已選對正確答案,其余題中有兩道只能分別判斷2個選項是錯誤的,還有1道題因不理解題意只好亂猜.
(1) 求該考生8道題全答對的概率;
(2)若評分標準規定:“每題只選一個選項,選對得5分,不選或選錯得0分”,求該考生所得分數的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)為了參加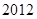 年貴州省高中籃球比賽,某中學決定從四個籃球較強的班級中選出
年貴州省高中籃球比賽,某中學決定從四個籃球較強的班級中選出 人組成男子籃球隊代表所在地區參賽,隊員來源人數如下表:
人組成男子籃球隊代表所在地區參賽,隊員來源人數如下表:
| 班級 | 高三(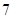 )班 )班 | 高三(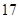 )班 )班 | 高二( )班 )班 | 高二(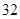 )班 )班 |
| 人數 |  | 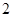 |  |  |
 名隊員中隨機選出兩名,求兩人來自同一班級的概率;(II)該中學籃球隊經過奮力拼搏獲得冠軍.若要求選出兩位隊員代表冠軍隊發言,設其中來自高三(7)班的人數為
名隊員中隨機選出兩名,求兩人來自同一班級的概率;(II)該中學籃球隊經過奮力拼搏獲得冠軍.若要求選出兩位隊員代表冠軍隊發言,設其中來自高三(7)班的人數為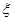 ,求隨機變量
,求隨機變量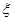 的分布列及數學期望
的分布列及數學期望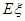 .
.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)設有關于 的一元二次方程
的一元二次方程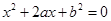 .
.
(1)若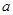 是從0,1,2,3四個數中任取的一個數,
是從0,1,2,3四個數中任取的一個數,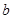 是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
(2)若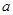 是從區間[0,3]任取的一個數,
是從區間[0,3]任取的一個數,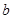 是從區間[0,2]任取的一個數,求上述方程有實根的概率.
是從區間[0,2]任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)
已知箱中裝有4個白球和5個黑球,且規定:取出一個白球的2分,取出一個黑球的1分.
現從該箱中任取 ( 無放回 ) 3個球,記隨機變量X為取出3球所得分數之和.
(Ⅰ) 求X的分布列;
(Ⅱ) 求X的數學期望E(X).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com