
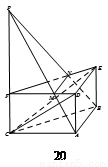
如圖,在正三棱柱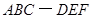 中,
中, 
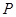 是
是 的沿長線上一點(diǎn),
的沿長線上一點(diǎn),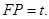 過
過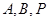 三點(diǎn)的平面交
三點(diǎn)的平面交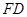 于
于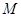 ,交
,交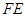 于
于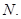
(Ⅰ)求證: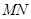 ∥平面
∥平面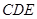 ;
;
(Ⅱ)當(dāng)平面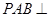 平面
平面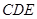 時,求
時,求 的值.
的值.
(Ⅰ)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052421563043755689/SYS201205242158222187770667_DA.files/image001.png">∥ ,
, 在平面
在平面 外,所以
外,所以 ∥平面
∥平面 ;……2分
;……2分
 是平面
是平面 與平面
與平面 的交線,所以
的交線,所以 ∥
∥ ,故
,故 ∥
∥ ;…………4分
;…………4分
而 在平面
在平面 外,所以
外,所以 ∥平面
∥平面 ……6分
……6分
注:不寫“ 在平面
在平面 外”等條件的應(yīng)酌情扣分;向量方法按建系、標(biāo)點(diǎn)、求向量、算結(jié)果這四個步驟是否正確來評分.
外”等條件的應(yīng)酌情扣分;向量方法按建系、標(biāo)點(diǎn)、求向量、算結(jié)果這四個步驟是否正確來評分.
(Ⅱ)解法一:取 中點(diǎn)
中點(diǎn) 、
、 中點(diǎn)
中點(diǎn) 則由
則由 ∥
∥ 知
知

 在同一平面上,并且由
在同一平面上,并且由 知
知 而與(Ⅰ)同理可證
而與(Ⅰ)同理可證 平行于平面
平行于平面 與平面
與平面 的交線,因此,
的交線,因此, 也垂直于該交線,但平面
也垂直于該交線,但平面 平面
平面 ,所以
,所以 平面
平面 ,
,
 …………8分
…………8分
于是, ∽
∽

 …………10分
…………10分
即 …………12分
…………12分
注:幾何解法的關(guān)鍵是將面面垂直轉(zhuǎn)化為線線垂直,閱卷時應(yīng)注意考生是否在運(yùn)用相關(guān)的定理.
(Ⅱ)解法二:如圖,取 中點(diǎn)
中點(diǎn) 、
、 中點(diǎn)
中點(diǎn) . 以
. 以 為原點(diǎn),
為原點(diǎn), 為
為 軸、
軸、 為
為 軸、
軸、 為
為 軸建立空間直角坐標(biāo)系.
軸建立空間直角坐標(biāo)系.
則在平面 中,
中, ,向量
,向量
設(shè)平面 的法向量
的法向量 ,則由
,則由 即
即
得 ………8分
………8分
在平面 中,
中, ,向量
,向量
設(shè)平面 的法向量
的法向量 ,由
,由
得 …10分
…10分
 平面
平面 平面
平面 ,
, ,即
,即 ………12分
………12分
注:使用其它坐標(biāo)系時請參考以上評分標(biāo)準(zhǔn)給分
【解析】略



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在正三棱柱中,AB=2,AA1=2由頂點(diǎn)B沿棱柱側(cè)面經(jīng)過棱AA1到頂點(diǎn)C1的最短路線與棱AA1的交點(diǎn)記為M,求:
如圖,在正三棱柱中,AB=2,AA1=2由頂點(diǎn)B沿棱柱側(cè)面經(jīng)過棱AA1到頂點(diǎn)C1的最短路線與棱AA1的交點(diǎn)記為M,求:| A1M | AM |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
如圖,在正三棱柱![]() 中,底面△
中,底面△![]() 的邊長為
的邊長為![]() ,
,![]() 為
為![]() 的中點(diǎn),三棱柱的體積
的中點(diǎn),三棱柱的體積![]() .
.
(1)求該三棱柱的側(cè)面積;
(2)求異面直線![]() 與
與![]() 所成角的大小(結(jié)果用反三角函數(shù)值表示)
所成角的大小(結(jié)果用反三角函數(shù)值表示)

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年江西南昌10所省高三第二次模擬沖刺理科數(shù)學(xué)試卷(二)(解析版) 題型:解答題
如圖,在正三棱柱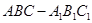 中,
中, ,
, 是
是 的中點(diǎn),
的中點(diǎn), 是線段
是線段 上的動點(diǎn)(與端點(diǎn)不重合),且
上的動點(diǎn)(與端點(diǎn)不重合),且 .
.

(1)若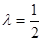 ,求證:
,求證: ;
;
(2)若直線 與平面
與平面 所成角的大小為
所成角的大小為 ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年福建省高三11月月考文科數(shù)學(xué)試卷 題型:填空題
如圖,在正三棱柱 中,D為棱
中,D為棱 的中點(diǎn),若截面
的中點(diǎn),若截面 是面積為6的直角三角形,則此三棱柱的體積為
。
是面積為6的直角三角形,則此三棱柱的體積為
。

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年西藏拉薩中學(xué)高三第七次月考考試?yán)砜茢?shù)學(xué) 題型:填空題
如圖,在正三棱柱 中,
中,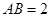 .若二面角
.若二面角 的大小為
的大小為 ,則點(diǎn)
,則點(diǎn) 到平面
到平面 的距離為
。
的距離為
。

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com