
【題目】某同學在研究性學習中,關于三角形與三角函數知識的應用(約定三內角![]() 所對的邊分別是
所對的邊分別是![]() )得出如下一些結論:
)得出如下一些結論:
(1)若![]() 是鈍角三角形,則
是鈍角三角形,則![]() ;
;
(2)若![]() 是銳角三角形,則
是銳角三角形,則![]() ;
;
(3)在三角形![]() 中,若
中,若![]() ,則
,則![]()
(4)在![]() 中,若
中,若![]() ,則
,則![]()
其中錯誤命題的個數是 ( )
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】(1)∵tanA+tanB=tan(A+B)(1tanAtanB),
∴tanA+tanB+tanC=tan(A+B)(1tanAtanB)+tanC=tanAtanBtanC,
∴△ABC是鈍角三角形,可得:tanAtanBtanC<0,故錯誤;
(2)∵△ABC為銳角三角形,
∴A+B>90°, B>90°A,
∴cosB<sinA,sinB>cosA,
∴cosBsinA<0,sinBcosA>0,
∴cosBsinA<sinBcosA,可得cosA+cosB<sinA+sinB,故錯誤;
(3)當![]() 時,tanB不存在,故錯誤;
時,tanB不存在,故錯誤;
(4)由![]() 得到0<C<90°,且
得到0<C<90°,且![]() ,
,
因為正切函數在(0,90°)為增函數,所以得到30°<C<45°;
由![]() 可得到0<B<90°或90°<B<180°,
可得到0<B<90°或90°<B<180°,
在0<B<90°時, ![]() ,因為正弦函數在(0,90°)為增函數,得到0<B<30°;
,因為正弦函數在(0,90°)為增函數,得到0<B<30°;
在90°<B<180°時, ![]() ,但是正弦函數在90°<B<180°為減函數,得到B>150°,則B+C>180°,
,但是正弦函數在90°<B<180°為減函數,得到B>150°,則B+C>180°,
矛盾,不成立。
所以0<B<30°.由B和C的取值得到A為鈍角,
所以A>C>B,故正確;
本題選擇D選項.


科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足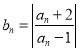 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表達式(不必寫出證明過程);
的表達式(不必寫出證明過程);
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
(B)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表達式(不必寫出證明過程);
的表達式(不必寫出證明過程);
(2)設![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A(4,-3),B(2,-1)和直線l:4x+3y-2=0.
(1)求在直角坐標平面內滿足|PA|=|PB|的點P的方程;
(2)求在直角坐標平面內一點P滿足|PA|=|PB|且點P到直線l的距離為2的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題錯誤的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 內一定存在直線平行于平面
內一定存在直線平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 內一定不存在直線垂直于平面
內一定不存在直線垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 內所有直線都垂直于平面
內所有直線都垂直于平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 是自然對數的底數.
是自然對數的底數.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .求實數
.求實數![]() 的值;
的值;
(2)①若![]() 時,函數
時,函數![]() 既有極大值,又有極小值,求實數
既有極大值,又有極小值,求實數![]() 的取值范圍;
的取值范圍;
②若![]() ,若
,若![]() 對一切正實數
對一切正實數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍(用
的取值范圍(用![]() 表示).
表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是公差為
是公差為![]() 的等差數列,
的等差數列,![]() 是公比為
是公比為![]() 的等比數列. 記
的等比數列. 記![]() .
.
(1)求證: 數列![]() 為等比數列;
為等比數列;
(2)已知數列![]() 的前
的前![]() 項分別為
項分別為![]() .
.
①求數列![]() 和
和![]() 的通項公式;
的通項公式;
②是否存在元素均為正整數的集合![]() ,使得數列
,使得數列![]() 等差數列?證明你的結論.
等差數列?證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com