
【題目】已知橢圓![]() :
: ![]() 的左焦點為
的左焦點為![]() ,
, ![]() 為坐標原點,點
為坐標原點,點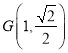 在橢圓上,過點
在橢圓上,過點![]() 的直線
的直線![]() 交橢圓于不同的兩點
交橢圓于不同的兩點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)求弦![]() 的中點
的中點![]() 的軌跡方程;
的軌跡方程;
(3)設過點![]() 且不與坐標軸垂直的直線交橢圓于
且不與坐標軸垂直的直線交橢圓于![]() 兩點,
兩點, ![]() 為
為![]() 軸上一點,若
軸上一點,若![]() 是菱形的兩條鄰邊,求點
是菱形的兩條鄰邊,求點![]() 橫坐標的取值范圍.
橫坐標的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】試題分析:(1)已知橢圓![]() :
: ![]() 的左焦點為
的左焦點為![]() ,有
,有![]() ,點
,點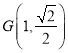 在橢圓上,得
在橢圓上,得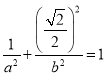 ,聯立求出
,聯立求出![]() 即得方程(2)設
即得方程(2)設![]() ,
, ![]() ,則
,則![]() ,當
,當![]() 時,
時, ![]() 點的坐標為
點的坐標為![]() . 當
. 當![]() 時,∵
時,∵![]() ,
, ![]() ,點差法兩式相減得
,點差法兩式相減得![]() ,
,
∴![]() ,又
,又![]() 過
過![]() 點,于是
點,于是![]() 的斜率為
的斜率為![]() ,∴
,∴![]() 整理即可
整理即可
(3)設![]() ,
, ![]() 的中點
的中點![]() ,由(2)知,
,由(2)知, ![]() ①
①
∵![]() ,∴
,∴![]() .∴
.∴![]() ,即
,即![]() ,整理得
,整理得![]() ②將②代入①中,得
②將②代入①中,得![]() ,化為
,化為![]() ,
,
∵![]() ,∴
,∴![]() ,由
,由![]() 得
得![]() 的范圍,從而得m的范圍.
的范圍,從而得m的范圍.
試題解析:
(1)由題意有![]() ,且
,且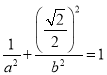 ,解得
,解得![]() ,
,
∴橢圓![]() 的方程為
的方程為![]() .
.
(2)設![]() ,
, ![]() ,則
,則![]() ,
,
當![]() 時,
時, ![]() 點的坐標為
點的坐標為![]() .
.
當![]() 時,∵
時,∵![]() ,
, ![]() ,
,
兩式相減得![]() ,
,
∴![]() ,又
,又![]() 過
過![]() 點,于是
點,于是![]() 的斜率為
的斜率為![]() ,
,
∴![]() ,
,
整理得![]() .
.
∵![]() 也滿足上式,
也滿足上式,
∴![]() 的軌跡方程為
的軌跡方程為![]() .
.
(3)設![]() ,
, ![]() 的中點
的中點![]() ,由(2)知,
,由(2)知, ![]() ①
①
∵![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() ,整理得
,整理得![]() ②
②
將②代入①中,得![]() ,化為
,化為![]() ,
,
∵![]() ,∴
,∴ ![]() ,
,
由![]() (當
(當![]() 時,
時, ![]() 與
與![]() 軸垂直,不合題意,舍去),得
軸垂直,不合題意,舍去),得![]() ,
,
于是![]() ,即
,即![]() 點的橫坐標的取值范圍為
點的橫坐標的取值范圍為![]() .
.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,點A是以線段BC為直徑的圓O上一點,AD⊥BC于點D,過點B作圓O的切線,與CA的延長線相交于點E,點G是AD的中點,連接CG并延長與BE相交于點F,延長AF與CB的延長線相交于點P. 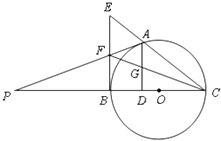
(1)求證:BF=EF;
(2)求證:PA是圓O的切線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合![]() .如果對于
.如果對于![]() 的每一個含有
的每一個含有![]() 個元素的子集
個元素的子集![]() ,
, ![]() 中必有4個元素的和等于
中必有4個元素的和等于![]() ,稱正整數
,稱正整數![]() 為集合
為集合![]() 的一個“相關數”.
的一個“相關數”.
(Ⅰ)當![]() 時,判斷5和6是否為集合
時,判斷5和6是否為集合![]() 的“相關數”,說明理由;
的“相關數”,說明理由;
(Ⅱ)若![]() 為集合
為集合![]() 的“相關數”,證明:
的“相關數”,證明: ![]() ;
;
(Ⅲ)給定正整數![]() .求集合
.求集合![]() 的“相關數”
的“相關數” ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了響應教育部頒布的《關于推進中小學生研學旅行的意見》,某校計劃開設八門研學旅行課程,并對全校學生的選擇意向進行調查(調查要求全員參與,每個學生必須從八門課程中選出唯一一門課程).本次調查結果整理成條形圖如下.

上圖中,已知課程![]() 為人文類課程,課程
為人文類課程,課程![]() 為自然科學類課程.為進一步研究學生選課意向,結合上面圖表,采取分層抽樣方法從全校抽取
為自然科學類課程.為進一步研究學生選課意向,結合上面圖表,采取分層抽樣方法從全校抽取![]() 的學生作為研究樣本組(以下簡稱“組M”).
的學生作為研究樣本組(以下簡稱“組M”).
(Ⅰ)在“組M”中,選擇人文類課程和自然科學類課程的人數各有多少?
(Ⅱ)為參加某地舉辦的自然科學營活動,從“組M”所有選擇自然科學類課程的同學中隨機抽取4名同學前往,其中選擇課程F或課程H的同學參加本次活動,費用為每人1500元,選擇課程G的同學參加,費用為每人2000元.
(ⅰ)設隨機變量![]() 表示選出的4名同學中選擇課程
表示選出的4名同學中選擇課程![]() 的人數,求隨機變量
的人數,求隨機變量![]() 的分布列;
的分布列;
(ⅱ)設隨機變量![]() 表示選出的4名同學參加科學營的費用總和,求隨機變量
表示選出的4名同學參加科學營的費用總和,求隨機變量![]() 的期望.
的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+ ![]() +b,其中a,b是常數且a>0.
+b,其中a,b是常數且a>0.
(1)用函數單調性的定義證明f(x)在區間(0, ![]() ]上是單調遞減函數;
]上是單調遞減函數;
(2)已知函數f(x)在區間[ ![]() ,+∞)上是單調遞增函數,且在區間[1,2]上f(x)的最大值為5,最小值為3,求a的值.
,+∞)上是單調遞增函數,且在區間[1,2]上f(x)的最大值為5,最小值為3,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (x≠0).
(x≠0).
(1)證明函數f(x)為奇函數;
(2)判斷函數f(x)在[1,+∞)上的單調性,并說明理由;
(3)若x∈[﹣2,﹣3],求函數的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
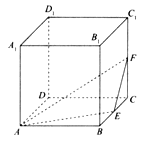
【題目】(文科選做)如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點E、F分別是棱BC,CC1的中點,P是側面BCC1B1內一點,若A1P∥平面AEF,則線段A1P長度的取值范圍是_____。
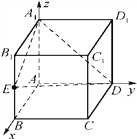
(理科選做)在正方體ABCD-A1B1C1D1中,點E為BB1的中點,則平面A1ED與平面ABCD所成的銳二面角的余弦值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且當x=
)的最小正周期是π,且當x= ![]() 時,f(x)取得最大值2.
時,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的圖象(要列表);
(2)將函數f(x)的圖象向右平移m(m>0)個單位長度后得到函數y=g(x)的圖象,且y=g(x)是偶函數,求m的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若關于x的不等式(a2﹣a)4x﹣2x﹣1<0在區間(﹣∞,1]上恒成立,則實數a的取值范圍為( )
A.(﹣2, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,6]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com