Question

【題目】已知為橢圓的左右焦點，點在橢圓上，且.

（1）求橢圓的方程；

（2）過的直線分別交橢圓于和，且，問是否存在常數(shù)，使得等差數(shù)列？若存在，求出的值，若不存在，請說明理由.

Answer 1

【答案】(1) ；(2)答案見解析.

【解析】試題分析：

（1）由已知可得，將 代入 可得；

（2）①當(dāng)的斜率為零或斜率不存在時， =；

②當(dāng)的斜率存在且時， 的方程為，

代入橢圓方程，并化簡得．

設(shè)，應(yīng)用韋達(dá)定理，弦長公式

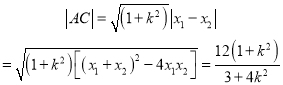
由直線的斜率為，得到，計算得到=，求得.

試題解析：

（1）因為，所以

所以 ，將P代入可得

所以橢圓的方程為

（2）①當(dāng)的斜率為零或斜率不存在時， =；

②當(dāng)的斜率存在且時， 的方程為，

代入橢圓方程，并化簡得．

設(shè)，則

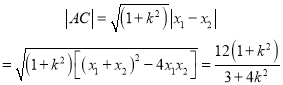
因為直線的斜率為，

所以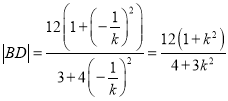

=

綜上，

所以，存在常數(shù)使得成等差數(shù)列.