
【題目】已知橢圓 ![]() 的右焦點(diǎn)為
的右焦點(diǎn)為 ![]() ,上頂點(diǎn)為
,上頂點(diǎn)為 ![]() ,
, ![]() 周長(zhǎng)為
周長(zhǎng)為 ![]() ,離心率為
,離心率為 ![]() .
.
(1)求橢圓 ![]() 的方程;
的方程;
(2)若點(diǎn) ![]() 是橢圓
是橢圓 ![]() 上第一象限內(nèi)的一個(gè)點(diǎn),直線(xiàn)
上第一象限內(nèi)的一個(gè)點(diǎn),直線(xiàn) ![]() 過(guò)點(diǎn)
過(guò)點(diǎn) ![]() 且與直線(xiàn)
且與直線(xiàn) ![]() 平行,直線(xiàn)
平行,直線(xiàn) ![]() 且
且 ![]() 與橢圓
與橢圓 ![]() 交于
交于 ![]() 兩點(diǎn),與
兩點(diǎn),與 ![]() 交于點(diǎn)
交于點(diǎn) ![]() ,是否存在常數(shù)
,是否存在常數(shù) ![]() ,使
,使 ![]() .若存在,求出
.若存在,求出 ![]() 的值,若不存在,請(qǐng)說(shuō)明理由.
的值,若不存在,請(qǐng)說(shuō)明理由.
【答案】
(1)解:由題意知 ![]() ,
, ![]() ,
,
又 ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
∴橢圓 ![]() 的方程為
的方程為 ![]() .
.
(2)解:由 ![]() 得
得 ![]() ,∴
,∴ ![]() ,
,
又 ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() 的方程為
的方程為 ![]() ,可設(shè)
,可設(shè) ![]() 方程為
方程為 ![]() ,
,
由 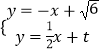 得
得 ![]() ,
,
由 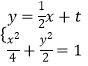 得
得 ![]() ,
, ![]() ,
, ![]() ,
,
設(shè) ![]() ,
, ![]() ,則
,則 ![]() ,
, ![]() ,
,
由弦長(zhǎng)公式: ![]() ,
,
同理, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴存在常數(shù) ![]() ,使
,使 ![]()
【解析】(1)考查了橢圓的幾何性質(zhì)與標(biāo)準(zhǔn)方程。
(2)考查了橢圓的綜合應(yīng)用、弦長(zhǎng)公式。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】將函數(shù) ![]() 的圖象向左平移
的圖象向左平移 ![]() 個(gè)單位,再向上平移1個(gè)單位,得到g(x)的圖象.若g(x1)g(x2)=9,且x1 , x2∈[﹣2π,2π],則2x1﹣x2的最大值為( )
個(gè)單位,再向上平移1個(gè)單位,得到g(x)的圖象.若g(x1)g(x2)=9,且x1 , x2∈[﹣2π,2π],則2x1﹣x2的最大值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】共享單車(chē)是指由企業(yè)在校園、公交站點(diǎn)、商業(yè)區(qū)、公共服務(wù)區(qū)等場(chǎng)所提供的自行車(chē)單車(chē)共享服務(wù),由于其依托“互聯(lián)網(wǎng)+”,符合“低碳出行”的理念,已越來(lái)越多地引起了人們的關(guān)注.某部門(mén)為了對(duì)該城市共享單車(chē)加強(qiáng)監(jiān)管,隨機(jī)選取了100人就該城市共享單車(chē)的推行情況進(jìn)行問(wèn)卷調(diào)查,并將問(wèn)卷中的這100人根據(jù)其滿(mǎn)意度評(píng)分值(百分制)按照[50,60),[60,70),…,[90,100]分成5組,制成如圖所示頻率分直方圖. 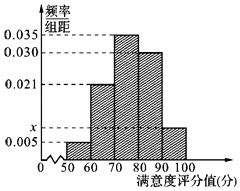
(Ⅰ) 求圖中x的值;
(Ⅱ) 已知滿(mǎn)意度評(píng)分值在[90,100]內(nèi)的男生數(shù)與女生數(shù)的比為2:1,若在滿(mǎn)意度評(píng)分值為[90,100]的人中隨機(jī)抽取4人進(jìn)行座談,設(shè)其中的女生人數(shù)為隨機(jī)變量X,求X的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】正三角形![]() 的邊長(zhǎng)為2,將它沿高
的邊長(zhǎng)為2,將它沿高![]() 翻折,使點(diǎn)
翻折,使點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 間的距離為
間的距離為![]() ,此時(shí)四面體
,此時(shí)四面體![]() 外接球表面積為__________.
外接球表面積為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知任意角
中,已知任意角![]() 以坐標(biāo)原點(diǎn)
以坐標(biāo)原點(diǎn)![]() 為頂點(diǎn),
為頂點(diǎn),![]() 軸的非負(fù)半軸為始邊,若終邊經(jīng)過(guò)點(diǎn)
軸的非負(fù)半軸為始邊,若終邊經(jīng)過(guò)點(diǎn)![]() ,且
,且![]() ,定義:
,定義:![]() ,稱(chēng)“
,稱(chēng)“![]() ”為“正余弦函數(shù)”,對(duì)于“正余弦函數(shù)
”為“正余弦函數(shù)”,對(duì)于“正余弦函數(shù)![]() ”,有同學(xué)得到以下性質(zhì):
”,有同學(xué)得到以下性質(zhì):
①該函數(shù)的值域?yàn)?/span>![]() ; ②該函數(shù)的圖象關(guān)于原點(diǎn)對(duì)稱(chēng);
; ②該函數(shù)的圖象關(guān)于原點(diǎn)對(duì)稱(chēng);
③該函數(shù)的圖象關(guān)于直線(xiàn)![]() 對(duì)稱(chēng); ④該函數(shù)為周期函數(shù),且最小正周期為
對(duì)稱(chēng); ④該函數(shù)為周期函數(shù),且最小正周期為![]() ;
;
⑤該函數(shù)的遞增區(qū)間為![]() .
.
其中正確的是__________.(填上所有正確性質(zhì)的序號(hào))
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系中,![]() ,
,![]() ,
,![]() (O是坐標(biāo)原點(diǎn)),其中
(O是坐標(biāo)原點(diǎn)),其中![]() 。
。
(1)求B點(diǎn)坐標(biāo);
(2)求四邊形OABC在第一象限部分面積![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】拋擲兩顆骰子,求:
(1)向上點(diǎn)數(shù)之和是![]() 的倍數(shù)的概率;
的倍數(shù)的概率;
(2)向上點(diǎn)數(shù)之和大于![]() 小于
小于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=cosx(![]() sinx+cosx)-
sinx+cosx)-![]() ,x∈R.
,x∈R.
(1)求函數(shù)f(x)的最小正周期和單調(diào)遞增區(qū)間;
(2)設(shè)![]() >0,若函數(shù)g(x)=f(x+
>0,若函數(shù)g(x)=f(x+![]() )為奇函數(shù),求
)為奇函數(shù),求![]() 的最小值.
的最小值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com