
【題目】為了解學生身高情況,某校以![]() 的比例對全校1000名學生按性別進行分層抽樣調查,已知男女比例為
的比例對全校1000名學生按性別進行分層抽樣調查,已知男女比例為![]() ,測得男生身高情況的頻率分布直方圖(如圖所示):
,測得男生身高情況的頻率分布直方圖(如圖所示):
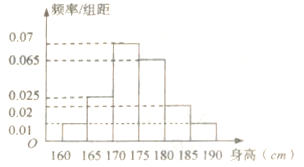
(1)計算所抽取的男生人數,并估計男生身高的中位數(保留兩位小數);
(2)從樣本中身高在![]() 之間的男生中任選2人,求至少有1人身高在
之間的男生中任選2人,求至少有1人身高在![]() 之間的概率.
之間的概率.
【答案】(1)174.64cm(2)![]() .
.
【解析】試題分析:
(1)由題意結合中位數的求法可得男生身高的中位數是174.64cm;
(2)列出所有可能的事件,結合古典概型公式可得至少有1人身高在![]() 之間的概率是
之間的概率是![]() .
.
試題解析:
(1)由題意得,所抽取的男生人數為:
1000×8%×![]() =40人
=40人
依據樣本頻率分布直方圖:0.01×5+0.025×5+x=0.5 得x=0.325 ,而身高170~175之間的頻率為0.35,所以中位數為170+5×![]() ≈174.64cm
≈174.64cm
(2)樣本中身高在180~185 cm之間的男生有4人,設其編號為①,②,③,④,樣本中身高在185~190 cm之間的男生有2人,設其編號為⑤,⑥,從上述6人中任取2人的共有:
(①,②)(①,③)(①,④)(①,⑤)(①,⑥)
(②,③)(②,④)(②,⑤)(②,⑥)
(③,④)(③,⑤)(③,⑥)
(④,⑤)(④,⑥)
(⑤,⑥)
故從樣本中身高在180~190 cm之間的男生中任選2人的所有可能結果數為15,至少有1人身高在185~190 cm之間的可能結果數為9,因此,所求概率P2=![]() =
=![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數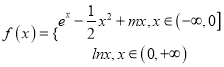 ,
, ![]() (
(![]() 為自然對數的底數).
為自然對數的底數).
(1)若函數![]() 的圖象在
的圖象在![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 時,函數
時,函數![]() 在
在![]() 內是增函數,求
內是增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,設函數
時,設函數![]() 的圖象
的圖象![]() 與函數
與函數![]() 的圖象
的圖象![]() 交于點
交于點![]() 、
、![]() ,過線段
,過線段![]() 的中點
的中點![]() 作
作![]() 軸的垂線分別交
軸的垂線分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,問是否存在點
,問是否存在點![]() ,使
,使![]() 在
在![]() 處的切線與
處的切線與![]() 在
在![]() 處的切線平行?若存在,求出
處的切線平行?若存在,求出![]() 的橫坐標;若不存在,請說明理由.
的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系下,曲線
軸的正半軸為極軸的極坐標系下,曲線![]() 的方程為
的方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 和曲線
和曲線![]() 的交點為
的交點為![]() 、
、![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一個食品商店為了調查氣溫對熱飲銷售的影響,經過調查得到關于賣出的熱飲杯數與當天氣溫的數據如下表,繪出散點圖如下.通過計算,可以得到對應的回歸方程![]() =-2.352x+147.767,根據以上信息,判斷下列結論中正確的是( )
=-2.352x+147.767,根據以上信息,判斷下列結論中正確的是( )
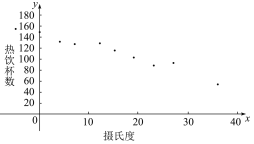
攝氏溫度 | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
熱飲杯數 | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
A.氣溫與熱飲的銷售杯數之間成正相關
B.當天氣溫為2℃時,這天大約可以賣出143杯熱飲
C.當天氣溫為10℃時,這天恰賣出124杯熱飲
D.由于x=0時,![]() 的值與調查數據不符,故氣溫與賣出熱飲杯數不存在線性相關性
的值與調查數據不符,故氣溫與賣出熱飲杯數不存在線性相關性
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的甲、乙兩個車間的![]() 名工人進行了勞動技能大比拼,規定:技能成績大于或等于
名工人進行了勞動技能大比拼,規定:技能成績大于或等于![]() 分為優秀,
分為優秀, ![]() 分以下為非優秀,統計成成績后,得到如下的
分以下為非優秀,統計成成績后,得到如下的![]() 列聯表,且已知在甲、乙兩個車間工人中隨機抽取
列聯表,且已知在甲、乙兩個車間工人中隨機抽取![]() 人為優秀的概率為
人為優秀的概率為![]() .
.
優秀 | 非優秀 | 合計 | |
甲車間 |
| ||
乙車間 |
| ||
合計 |
|
(1)請完成上面的列聯表;
(2)根據列聯表的數據,若按![]() 的可靠性要求,能否認為“成績與車間有關系”?
的可靠性要求,能否認為“成績與車間有關系”?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集為[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求證:ax+by+cz≤1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們知道:人們對聲音有不同的感覺,這與它的強度有關系.聲音的強度![]() 用瓦/米2 (
用瓦/米2 (![]() )表示,但在實際測量時,常用聲音的強度水平
)表示,但在實際測量時,常用聲音的強度水平![]() 表示,它們滿足以下公式:
表示,它們滿足以下公式: ![]() (單位為分貝,
(單位為分貝, ![]() ,其中
,其中![]() ,這是人們平均能聽到的最小強度,是聽覺的開端).回答以下問題:
,這是人們平均能聽到的最小強度,是聽覺的開端).回答以下問題:
(1)樹葉沙沙聲的強度是![]() ,耳語的強度是
,耳語的強度是![]() ,恬靜的無線電廣播的強度是
,恬靜的無線電廣播的強度是![]() ,試分別求出它們的強度水平;
,試分別求出它們的強度水平;
(2)某一新建的安靜小區規定:小區內公共場所的聲音的強度水平必須保持在50分貝以下,試求聲音強度![]() 的范圍為多少?
的范圍為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com