
【題目】已知函數(shù)f(x)= ![]() sinωxcosωx﹣cos2ωx﹣
sinωxcosωx﹣cos2ωx﹣ ![]() (ω>0,x∈R)的圖象上相鄰兩個(gè)最高點(diǎn)的距離為π.
(ω>0,x∈R)的圖象上相鄰兩個(gè)最高點(diǎn)的距離為π.
(Ⅰ)求函數(shù)f(x)的單調(diào)遞增區(qū)間;
(Ⅱ)若△ABC三個(gè)內(nèi)角A、B、C的對邊分別為a、b、c,且c= ![]() ,f(C)=0,sinB=3sinA,求a,b的值.
,f(C)=0,sinB=3sinA,求a,b的值.
【答案】解:f(x)= ![]() sin2ωx﹣
sin2ωx﹣ ![]() (1+cos2ωx)﹣
(1+cos2ωx)﹣ ![]() =sin(2ωx﹣
=sin(2ωx﹣ ![]() )﹣1,
)﹣1,
∵f(x)圖象上相鄰兩個(gè)最高點(diǎn)的距離為π,
∴ ![]() =π,即ω=1,
=π,即ω=1,
則f(x)=sin(2x﹣ ![]() )﹣1,
)﹣1,
(Ⅰ)令﹣ ![]() +2kπ≤2x﹣
+2kπ≤2x﹣ ![]() ≤
≤ ![]() +2kπ,k∈Z,得到﹣
+2kπ,k∈Z,得到﹣ ![]() +kπ≤x≤kπ+
+kπ≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
則函數(shù)f(x)的單調(diào)遞增區(qū)間為[﹣ ![]() +kπ,kπ+
+kπ,kπ+ ![]() ],k∈Z;
],k∈Z;
(Ⅱ)由f(C)=0,得到f(C)=sin(2C﹣ ![]() )﹣1=0,即sin(2x﹣
)﹣1=0,即sin(2x﹣ ![]() )=1,
)=1,
∴2C﹣ ![]() =
= ![]() ,即C=
,即C= ![]() ,
,
由正弦定理 ![]() =
= ![]() 得:b=
得:b= ![]() ,
,
把sinB=3sinA代入得:b=3a,
由余弦定理及c= ![]() 得:cosC=
得:cosC= ![]() =
= ![]() =
= ![]() ,
,
整理得:10a2﹣7=3a2 ,
解得:a=1,
則b=3.
【解析】(Ⅰ)f(x)解析式利用二倍角的正弦、余弦函數(shù)公式化簡,整理為一個(gè)角的正弦函數(shù),根據(jù)題意確定出ω的值,確定出f(x)解析式,利用正弦函數(shù)的單調(diào)性求出函數(shù)f(x)的單調(diào)遞增區(qū)間即可;(Ⅱ)由f(C)=0,求出C的度數(shù),利用正弦定理化簡sinB=3sinA,由余弦定理表示出cosC,把各自的值代入求出a與b的值即可.
【考點(diǎn)精析】本題主要考查了兩角和與差的正弦公式和正弦函數(shù)的單調(diào)性的相關(guān)知識點(diǎn),需要掌握兩角和與差的正弦公式:![]() ;正弦函數(shù)的單調(diào)性:在
;正弦函數(shù)的單調(diào)性:在![]()
![]() 上是增函數(shù);在
上是增函數(shù);在![]()
![]() 上是減函數(shù)才能正確解答此題.
上是減函數(shù)才能正確解答此題.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=ex , g(x)=kx+1.
(I)求函數(shù)y=f(x)﹣(x+1)的最小值;
(II)證明:當(dāng)k>1時(shí),存在x0>0,使對于任意x∈(0,x0)都有f(x)<g(x);
(III)若存在實(shí)數(shù)m使對任意x∈(0,m)都有|f(x)﹣g(x)|>x成立,求實(shí)數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a>0,函數(shù)f(x)= ![]() +|lnx﹣a|,x∈[1,e2].
+|lnx﹣a|,x∈[1,e2].
(1)當(dāng)a=3時(shí),求曲線y=f(x)在點(diǎn)(3,f(3))處的切線方程;
(2)若f(x)≤ ![]() 恒成立,求實(shí)數(shù)a的取值范圍.
恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某競賽的題庫系統(tǒng)有60%的自然科學(xué)類題目,40%的文化生活類題目(假設(shè)題庫中的題目總數(shù)非常大),參賽者需從題庫中抽取3個(gè)題目作答,有兩種抽取方法:方法一是直接從題庫中隨機(jī)抽取3個(gè)題目;方法二是先在題庫中按照題目類型用分層抽樣的方法抽取10個(gè)題目作為樣本,再從這10個(gè)題目中任意抽取3個(gè)題目.
(1)兩種方法抽取的3個(gè)題目中,恰好有1個(gè)自然科學(xué)類題目和2個(gè)文化生活類題目的概率是否相同?若相同,說明理由;若不同,分別計(jì)算出兩種抽取方法對應(yīng)的概率.
(2)已知某參賽者抽取的3個(gè)題目恰好有1個(gè)自然科學(xué)類題目和2個(gè)文化生活類題目,且該參賽者答對自然科學(xué)類題目的概率為![]() ,答對文化生活類題目的概率為
,答對文化生活類題目的概率為![]() .設(shè)該參賽者答對的題目數(shù)為X,求X的分布列和數(shù)學(xué)期望.
.設(shè)該參賽者答對的題目數(shù)為X,求X的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合M={(x,y)|y=f(x)},若對于任意(x1 , y1)∈M,存在(x2 , y2)∈M,使得x1x2+y1y2=0成立,則稱集合M是“垂直對點(diǎn)集”.給出下列四個(gè)集合:
①M(fèi)={ ![]() };
};
②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};
④M={(x,y)|y=ex﹣2}.
其中是“垂直對點(diǎn)集”的序號是( )
A.①②
B.②③
C.①④
D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】經(jīng)過對K2的統(tǒng)計(jì)量的研究,得到了若干個(gè)觀測值,當(dāng)K2≈6.706時(shí),我們認(rèn)為兩分類變量A、B( )
A. 有67.06%的把握認(rèn)為A與B有關(guān)系 B. 有99%的把握認(rèn)為A與B有關(guān)系
C. 有0.010的把握認(rèn)為A與B有關(guān)系 D. 沒有充分理由說明A與B有關(guān)系
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某程序框圖如圖所示,現(xiàn)輸入如下四個(gè)函數(shù),則可以輸出的函數(shù)是( ) 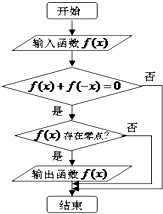
A.f(x)=x2
B.f(x)=sinx
C.f(x)=ex
D.f(x)= ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某產(chǎn)品的廣告費(fèi)用x與銷售額y的統(tǒng)計(jì)數(shù)據(jù)如下表:
廣告費(fèi)用x(萬元) | 4 | 2 | 3 | 5 |
銷售額y(萬元) | 49 | 26 | 39 | 54 |
(1)求根據(jù)上表可得線性回歸方程![]() =
=![]() x+
x+![]() ;
;
(2) 模型預(yù)報(bào)廣告費(fèi)用為6萬元時(shí)銷售額為多少
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù)f(x)=sin(x﹣![]() )sin(x+
)sin(x+![]() ),有下列命題:
),有下列命題:
①此函數(shù)可以化為f(x)=﹣![]() sin(2x+
sin(2x+![]() );
);
②函數(shù)f(x)的最小正周期是π,其圖象的一個(gè)對稱中心是(![]() , 0);
, 0);
③函數(shù)f(x)的最小值為﹣![]() , 其圖象的一條對稱軸是x=
, 其圖象的一條對稱軸是x=![]() ;
;
④函數(shù)f(x)的圖象向右平移![]() 個(gè)單位后得到的函數(shù)是偶函數(shù);
個(gè)單位后得到的函數(shù)是偶函數(shù);
⑤函數(shù)f(x)在區(qū)間(﹣![]() , 0)上是減函數(shù).
, 0)上是減函數(shù).
其中所有正確的命題的序號個(gè)數(shù)是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com