
【題目】已知函數![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,若關于
時,若關于![]() 的方程
的方程![]() 有唯一實數解,試求實數
有唯一實數解,試求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 有兩個極值點
有兩個極值點![]() ,
,![]() ,且不等式
,且不等式![]() 恒成立,試求實數
恒成立,試求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)對函數![]() 求導,求出
求導,求出![]() 的值可得切點坐標,求出
的值可得切點坐標,求出![]() 的值,可得切線斜率,利用點斜式可得在點
的值,可得切線斜率,利用點斜式可得在點![]() 的切線方程;(2)原方程等價于
的切線方程;(2)原方程等價于![]() ,對
,對![]() 求導得到函數
求導得到函數![]() 單調區間,可知當
單調區間,可知當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,結合單調性可得到實數
,結合單調性可得到實數![]() 的取值范圍;(3)對函數
的取值范圍;(3)對函數![]() 求導,可得
求導,可得![]() ,
,![]() 恒成立
恒成立![]() 恒成立,將
恒成立,將![]() 用
用![]() 替換,并構造函數
替換,并構造函數![]() ,對
,對![]() 求導可求得函數
求導可求得函數![]() 在
在![]() 上的最小值,即可知道實數
上的最小值,即可知道實數![]() 的取值范圍.
的取值范圍.
(1)當![]() 時,有
時,有![]() ,
,
![]() ,
,
![]() ,
,
![]() 過點
過點![]() 的切線方程為
的切線方程為![]() ,即
,即![]() .
.
(2)當![]() 時,有
時,有![]() ,其定義域為
,其定義域為![]() ,
,
從而方程![]() ,可化為
,可化為![]() ,令
,令![]() ,
,
則![]() ,
,
由![]() 或
或![]() ,
,
![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
且![]() ,
,
又當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
![]() 關于
關于![]() 的方程
的方程![]() 有唯一實數解,所以實數
有唯一實數解,所以實數![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .
.
(3)![]() 的定義域為
的定義域為![]() ,
,
令![]() ,
,
又因為函數![]() 有兩個極值點
有兩個極值點![]() ,
,
![]() 有兩個不等實數根
有兩個不等實數根![]() ,
,
![]() ,且
,且![]() ,
,
從而![]() ,
,
由不等式![]() 恒成立
恒成立![]() 恒成立,
恒成立,
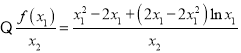
![]() ,
,
令![]() ,
,![]() ,
,
當![]() 時恒成立,所以函數
時恒成立,所以函數![]() 在
在![]() 上單調遞減,
上單調遞減,![]() ,故實數
,故實數![]() 的取值范圍是
的取值范圍是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數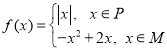 ,其中
,其中![]() 、
、![]() 是非空數集,且
是非空數集,且![]() ,設
,設![]() ,
,![]() ;
;
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)是否存在實數![]() ,使得
,使得![]() ,且
,且![]() ?若存在,請求出滿足條件的實數
?若存在,請求出滿足條件的實數![]() ;若不存在,請說明理由;
;若不存在,請說明理由;
(3)若![]() ,且
,且![]() ,
,![]() ,
,![]() 是單調遞增函數,求集合
是單調遞增函數,求集合![]() 、
、![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司利用簡單隨機抽樣方法,對投保車輛進行抽樣,樣本車輛中每輛車的賠付結果統計如下:
賠付金額(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
車輛數(輛) | 500 | 130 | 100 | 150 | 120 |
(1)若每輛車的投保金額均為2800元,估計賠付金額大于投保金額的概率.
(2)在樣本車輛中,車主是新司機的占10%,在賠付金額為4000元的樣本車輛中,車主是新司機的占20%,估計在已投保車輛中,新司機獲賠金額為4000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】趙爽是我國古代數學家、天文學家大約在公元222年趙爽為《周碑算經》一書作序時,介紹了“勾股圓方圖”,亦稱“趙爽弦圖”(以弦為邊長得到的正方形是由4個全等的直角三角形再加上中間的一個小正方形組成的)類比“趙爽弦圖”,趙爽弦圖可類似地構造如圖所示的圖形,它是由個3全等的等邊三角形與中間的一個小等邊三角形組成的一個大等邊三角形,設DF2AF,若在大等邊三角形中隨機取一點,則此點取自小等邊三角形的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com